图的最短路径算法

Algorithm

发布日期: 2021-01-22

更新日期: 2022-07-31

文章字数: 2k

阅读时长: 10 分

阅读次数:

引言：

图的最短路径问题是求图中两顶点间的最短路径问题。

在网图和非网图中，最短路径的含义不同。由于非网图它没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径；而对于网图来说，最短路径是指两顶点之间经过的边上权值之和最少的路径，并且将路径上的第一个顶点称为源点，最后一个顶点称为终点。其实非网图完全可以理解成所有边的权值都为1的网。

迪杰斯特拉（Dijkstra）算法

这是一个按路径长度递增的次序产生最短路径的算法。并不是一下子求出两顶点间的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到想要的结果。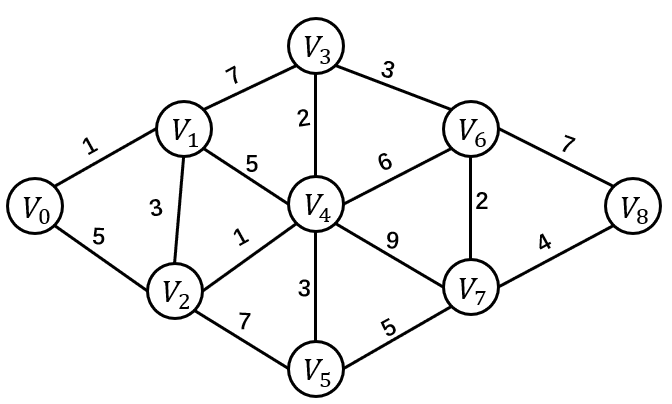

//图数据结构（邻接矩阵的方式）
class Graph {
    final int INFINITY = Integer.MAX_VALUE;//很大很大的数
    int vexNum = 9;//顶点数目
    //邻接矩阵
    int[][] adj = {{0, 1, 5, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY},
            {1, 0, 3, 7, 5, INFINITY, INFINITY, INFINITY, INFINITY},
            {5, 3, 0, INFINITY, 1, 7, INFINITY, INFINITY, INFINITY},
            {INFINITY, 7, INFINITY, 0, 2, INFINITY, 3, INFINITY, INFINITY},
            {INFINITY, 5, 1, 2, 0, 3, 6, 9, INFINITY},
            {INFINITY, INFINITY, 7, INFINITY, 3, 0, INFINITY, 5, INFINITY},
            {INFINITY, INFINITY, INFINITY, 3, 6, INFINITY, 0, 2, 7},
            {INFINITY, INFINITY, INFINITY, INFINITY, 9, 5, 2, 0, 4},
            {INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, 7, 4, 0}};
}

public class GrapTest {
    @Test
    public void testDijkstra() {
        Graph g = new Graph();
        int from = 0;//起点
        List<int[]> ans = new Dijkstra().shortestPath(g, from);
        int[] shortDis = ans.get(0);
        int[] path = ans.get(1);
        new Dijkstra().showPath(g, from, shortDis, path);
    }
}

//迪杰斯特拉（Dijkstra）算法，计算起点到其他点的最短路径 O(n^2)
class Dijkstra{
    public List<int[]> shortestPath(Graph g, int from) {
        int[] D = new int[g.vexNum];   //D[w]表示顶点到from的最短路径
        int[] P = new int[g.vexNum];   //P[w]表示最后到达w经过的顶点，即最后一步为P[w]-->w
        int[] find = new int[g.vexNum];//find[w]=1表示求得顶点from至w的最短路径
        //初始化数据
        for (int v = 0; v < g.vexNum; v++) {
            D[v] = g.adj[from][v];
            P[v] = from;
        }
        D[from] = 0;
        find[from] = 1;

        //开始主循环，每次求得from到某个顶点v的最短路径
        int k=0;
        long min;
        for (int v = 0; v < g.vexNum; v++) {
            min = Integer.MAX_VALUE;
            for (int w = 0; w < g.vexNum; w++) {
                if (find[w] == 0 && D[w] < min) {
                    min = D[w];
                    k = w;
                }
            }
            find[k] = 1;//表示已求得from到k的最短路径
            /*当顶点from到k的目前最短距离找到后，k到w若还有距离，就得考虑是否要修改D[w]。因为from到k的距离加上k到w的距离可能小于当前的D[w]*/
            for (int w = 0; w < g.vexNum; w++) {
                if (find[w] == 0 && (min + g.adj[k][w]) < D[w]) {
                    D[w] = (int)min + g.adj[k][w];
                    P[w] = k;//k到w若还有距离，就得考虑是否要修改D[w]。因为from到k的距离加上k到w的距离可能小于当前的D[w]
                }
            }
        }
         return Arrays.asList(D, P);
    }

    public void showPath(Graph g, int from, int[] D, int[] P) {
        //打印shortDis数组
        Arrays.stream(D).forEach(each -> System.out.print(each + " "));
        System.out.println();
        //打印从from顶点到各顶点最短距离的路径
        for (int i = 0; i < g.vexNum; i++) {
            int a = i;
            System.out.print(a + " <-- ");
            while ((a = P[a]) != from) {
                System.out.print(a+" <-- ");
            }
            System.out.println(from);
        }
    }
}

0 1 4 7 5 8 10 12 16
0 <-- 0
1 <-- 0
2 <-- 1 <-- 0
3 <-- 4 <-- 2 <-- 1 <-- 0
4 <-- 2 <-- 1 <-- 0
5 <-- 4 <-- 2 <-- 1 <-- 0
6 <-- 3 <-- 4 <-- 2 <-- 1 <-- 0
7 <-- 6 <-- 3 <-- 4 <-- 2 <-- 1 <-- 0
8 <-- 7 <-- 6 <-- 3 <-- 4 <-- 2 <-- 1 <-- 0

通过迪杰斯特拉（Dijkstra）算法，可以解决从某个顶点到其余各顶点的最短路径问题。从循环嵌套可以很容易得到此算法的时间复杂度为 O(n²)。能不能只找到从源点到某一个特定终点的最短路径呢？其实这个问题和求解源点到其他所有顶点的最短路径一样复杂，时间复杂度依然是 O(n²)。
如果需要知道V₃到V₅、V₁到V₇这样的任一顶点到其余所有顶点的最短路径怎么办呢？此时简单的办法就是对每个顶点当做源点运行一次迪杰斯特拉（Dijktra）算法，等于在原有算法的基础上，再来一个循环，此时整个算法的时间复杂度就成了 O(n³)。

弗洛伊德（Floyd）算法

该算法求得所有顶点到所有顶点的最短路径的时间复杂度也是 O(n³)，但其算法非常简洁优雅。

//图数据结构（邻接矩阵的方式）
class Graph {
    final int INFINITY = Integer.MAX_VALUE;//很大很大的数
    int vexNum = 9;//顶点数目
    //邻接矩阵
    int[][] adj = {{0, 1, 5, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY},
            {1, 0, 3, 7, 5, INFINITY, INFINITY, INFINITY, INFINITY},
            {5, 3, 0, INFINITY, 1, 7, INFINITY, INFINITY, INFINITY},
            {INFINITY, 7, INFINITY, 0, 2, INFINITY, 3, INFINITY, INFINITY},
            {INFINITY, 5, 1, 2, 0, 3, 6, 9, INFINITY},
            {INFINITY, INFINITY, 7, INFINITY, 3, 0, INFINITY, 5, INFINITY},
            {INFINITY, INFINITY, INFINITY, 3, 6, INFINITY, 0, 2, 7},
            {INFINITY, INFINITY, INFINITY, INFINITY, 9, 5, 2, 0, 4},
            {INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, INFINITY, 7, 4, 0}};
}

public class GrapTest {
    @Test
    public void testFloyd(){
        Graph g = new Graph();
        List<int[][]> ans = new Floyd().shortestPath(g);
        int[][] shortDis = ans.get(0);
        int[][] path = ans.get(1);
        new Floyd().showPath(g, shortDis, path);
    }
}

//弗洛伊德（Floyd）算法，计算任意两顶点间的最短路径 O(n^3)
class Floyd{
    public List<int[][]> shortestPath(Graph g) {
        int[][] D = new int[g.vexNum][g.vexNum];//顶点到顶点的最短路径长度
        int[][] P = new int[g.vexNum][g.vexNum];//对应顶点的最小路径的前驱矩阵
        int v, w;
        for (v = 0; v < g.vexNum; v++) {/*初始化D与P*/
            for (w = 0; w < g.vexNum; w++) {
                D[v][w] = g.adj[v][w];
                P[v][w] = w;
            }
        }
        int k;
        for (k = 0; k < g.vexNum; k++) {
            for (v = 0; v < g.vexNum; v++) {
                for (w = 0; w < g.vexNum; w++) {
                    if (D[v][k] == g.INFINITY || D[k][w] == g.INFINITY) continue;
                    if (D[v][w] > D[v][k] + D[k][w]) {
                        //如果经过下标为k顶点路径比原两顶点路径更短，将当前两点间权值设为更小的一个
                        D[v][w] = D[v][k] + D[k][w];
                        P[v][w] = P[v][k];/*路径设置为经过下标k的顶点*/
                    }
                }
            }
        }
        return Arrays.asList(D, P);
    }

    public void showPath(Graph g, int[][] D, int[][] P) {
        int v, w, k;
        for (v = 0; v < g.vexNum; ++v) {
            for (w = v + 1; w < g.vexNum; ++w) {
                System.out.print("[" + v + "]" + "--" + D[v][w] + "-->[" + w + "]: ");
                k = P[v][w];
                System.out.print(v + " -> ");
                while (k != w) {
                    System.out.print(k + " -> ");
                    k = P[k][w];
                }
                System.out.println(w);
            }
        }
    }
}

[0]--1-->[1]: 0 -> 1
[0]--4-->[2]: 0 -> 1 -> 2
[0]--7-->[3]: 0 -> 1 -> 2 -> 4 -> 3
[0]--5-->[4]: 0 -> 1 -> 2 -> 4
[0]--8-->[5]: 0 -> 1 -> 2 -> 4 -> 5
[0]--10-->[6]: 0 -> 1 -> 2 -> 4 -> 3 -> 6
[0]--12-->[7]: 0 -> 1 -> 2 -> 4 -> 3 -> 6 -> 7
[0]--16-->[8]: 0 -> 1 -> 2 -> 4 -> 3 -> 6 -> 7 -> 8
[1]--3-->[2]: 1 -> 2
[1]--6-->[3]: 1 -> 2 -> 4 -> 3
[1]--4-->[4]: 1 -> 2 -> 4
[1]--7-->[5]: 1 -> 2 -> 4 -> 5
[1]--9-->[6]: 1 -> 2 -> 4 -> 3 -> 6
[1]--11-->[7]: 1 -> 2 -> 4 -> 3 -> 6 -> 7
[1]--15-->[8]: 1 -> 2 -> 4 -> 3 -> 6 -> 7 -> 8
[2]--3-->[3]: 2 -> 4 -> 3
[2]--1-->[4]: 2 -> 4
[2]--4-->[5]: 2 -> 4 -> 5
[2]--6-->[6]: 2 -> 4 -> 3 -> 6
[2]--8-->[7]: 2 -> 4 -> 3 -> 6 -> 7
[2]--12-->[8]: 2 -> 4 -> 3 -> 6 -> 7 -> 8
[3]--2-->[4]: 3 -> 4
[3]--5-->[5]: 3 -> 4 -> 5
[3]--3-->[6]: 3 -> 6
[3]--5-->[7]: 3 -> 6 -> 7
[3]--9-->[8]: 3 -> 6 -> 7 -> 8
[4]--3-->[5]: 4 -> 5
[4]--5-->[6]: 4 -> 3 -> 6
[4]--7-->[7]: 4 -> 3 -> 6 -> 7
[4]--11-->[8]: 4 -> 3 -> 6 -> 7 -> 8
[5]--7-->[6]: 5 -> 7 -> 6
[5]--5-->[7]: 5 -> 7
[5]--9-->[8]: 5 -> 7 -> 8
[6]--2-->[7]: 6 -> 7
[6]--6-->[8]: 6 -> 7 -> 8
[7]--4-->[8]: 7 -> 8

弗洛伊德（Floyd）算法的代码非常简洁，是一个二重循环初始化加一个三重循环权值修正，其完成了所有顶点到所有顶点的最短路径计算。但是很可惜，它的时间复杂度是 O(n³)。

YangChongZhi

http://yczlab.top/posts/6a16f47a.html