连通图的最小生成树算法

Java Algorithm DataStructure
Algorithm
发布日期:   2021-01-21
更新日期:   2022-07-31
文章字数:   4k
阅读时长:   16 分
阅读次数:  

  

引言：

在线性表中，数据元素之间是被串起来的，仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继。在树形结构中，数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素相关，但只能和上一层中一个元素想关。这和一对父母可以有多个孩子，但每个孩子却只能有一对父母是一个道理。可现实中，人与人之间关系就非常复杂，比如我认识的朋友，可能他们之间也相互认识，这就不是简单的一对一、一对多的关系，研究人际关系很自然就会考虑到多对多的情况。也就是这篇博客的主题——图。图是一种较线性表和树更加复杂的数据结构。在图形结构中，节点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。

一、图的相关定义

1、图：

  图（Grap）是由顶点的有穷非空集合和顶点之间的边集合组成，通常表示为：G（V,E），其中，G表示一个图；V是图G中顶点的集合；E是图G中边的集合。

  • 通常线性表中我们把数据元素叫做元素，树中将数据元素叫做结点，在图中数据元素，则称之为顶点（Vertex）。
  • 线性表中可以没有数据元素，称为空表。树中可以没有结点，叫做空树。但是在图结构中，不允许没有顶点。在定义中，若 V 是顶点的集合，则强调了顶点集合 V 有穷非空。
  • 在线性表中，相邻的数据元素之间具有线性关系；在树结构中，相邻两层的结点具有层次关系。而在图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

2、无向边：

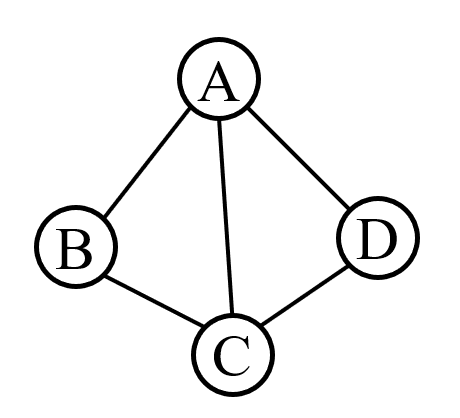
示意图 说明
若顶点 Vi 到 Vj 之间的边没有方向，则称这条边为无向边（Edge），用无序偶对（Vi,Vj）来表示。如果图中任意两个顶点之间的边都是无向边，则称该图为无向图。左侧就是一个无向图，由于是无方向的，连接顶点A与D的边，可以表示成无序对（A,D），也可以写成（D,A）。

3、有向边：

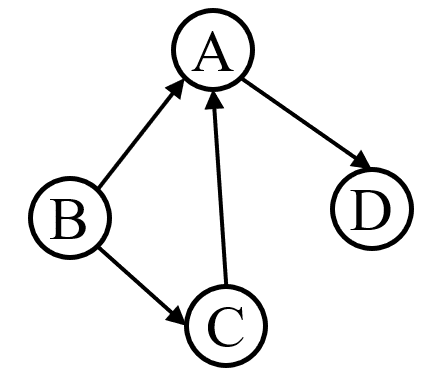
示意图 说明
若从顶点 Vi 到 Vj 之间的边有方向，则这条边为有向边，也称为弧（Arc）。用有序偶<Vi,Vj>来表示，Vi称为弧尾（Tail），Vj称为弧头（Head）。如果图中任意两个顶点之间的边都是有向边，则称该图为有向图。左图就是一个有向图，连接顶点A到D的有向边就是弧，A是弧尾，D是弧头，<A,D>表示该弧，不能写成<D,A>

4、简单图：

  • 在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

5、完全图：

  • 在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有n个顶点的无向完全图有n*(n-1)/2条边。
  • 在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。含有n个顶点的有向完全图有n*(n-1)条边。
  • 这里可以得出结论，对于具有n个顶点和e条边数的图，无向图 0≤e≤n(n-1)/2，有向图 0≤e≤n(n-1)

6、网（带权图）

有些图的边或者弧具有与它相关的数字，这种与图的边或弧相关的数叫做权（Weight）。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网。

7、子图

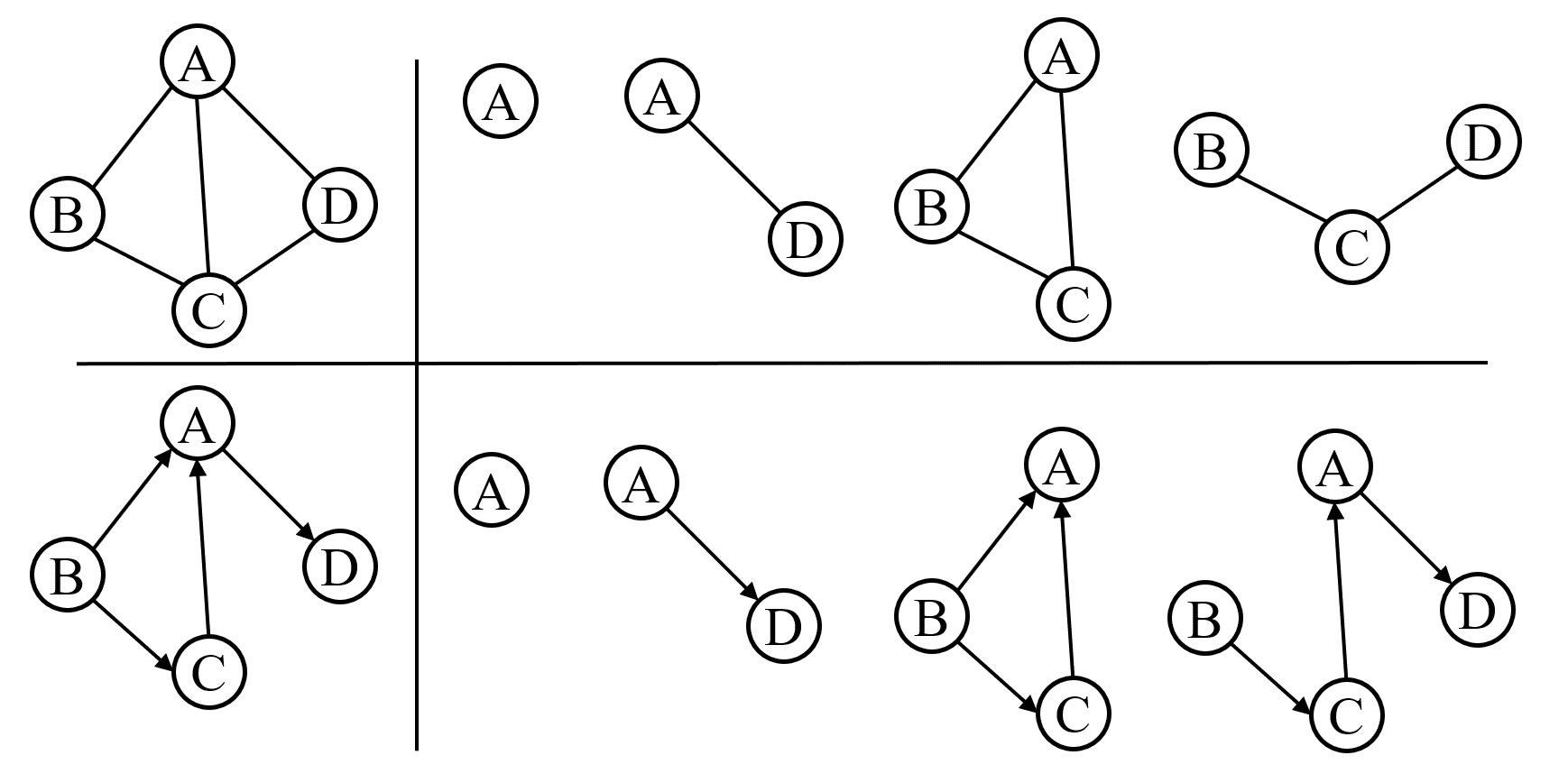
示意图 说明
假设有两个图 G = (V,{E})和 G‘ = (V‘,{E‘})，如果V‘∈V且E‘∈E，则称G‘为G的子图。例如左侧所示的有向图和无向图的子图。

8、图的顶点与边之间的关系

对于无向图：
  无向图 G = (V,{E})，如果边(V,V‘)∈E，则称顶点V和V‘互为邻接点（Adjacent），即V和V‘相邻接。边(V,V‘)依附（incident）于顶点V和V‘，或者说(V,V‘)与顶点V和V‘相关联。顶点V的度（Degree）是和V相关联的边的数目，记为 TD(V)。如上图A与B互为邻接点，边（A,B）依附于顶点A与B上，顶点A的度为3。其实边数就是各顶点度数和的一半，多出的一半是因为重复计数了。

对于有向图：
  有向图 G = (V,{E})，如果弧<V,V‘>∈E，则称顶点V邻接到顶点V‘，顶点V‘邻接自顶点V。弧<V,V‘>和顶点V，V‘相关联。以顶点v为头的弧的数目称为V的入度，记为 ID(V)；以V为尾的弧的数目称为V的出度，记为OD(V)；顶点V的度为TD(V)=ID(V)+OD(V)。其实边数就是各顶点的出度和，也是各顶点的入度和。

9、路径和环

  无向图 G = (V,{E}) 中从顶点V到顶点V‘的路径是一个顶点序列(V=Vi,0,Vi,1······Vi,m=V‘)，其中(Vi,j-1,Vi,j)∈E，1≤j≤m。如果 G 是有向图，则路径也是有向的，顶点序列应满足<Vi,j-1,Vi,j>∈E，1≤j≤m。
  树中根结点到任意结点的路径是唯一的，但是图中顶点与顶点之间的路径却是不唯一的。路径的长度是路径上的边或弧的数目。第一个顶点到最后一个顶点相同的路径称为回路或环。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。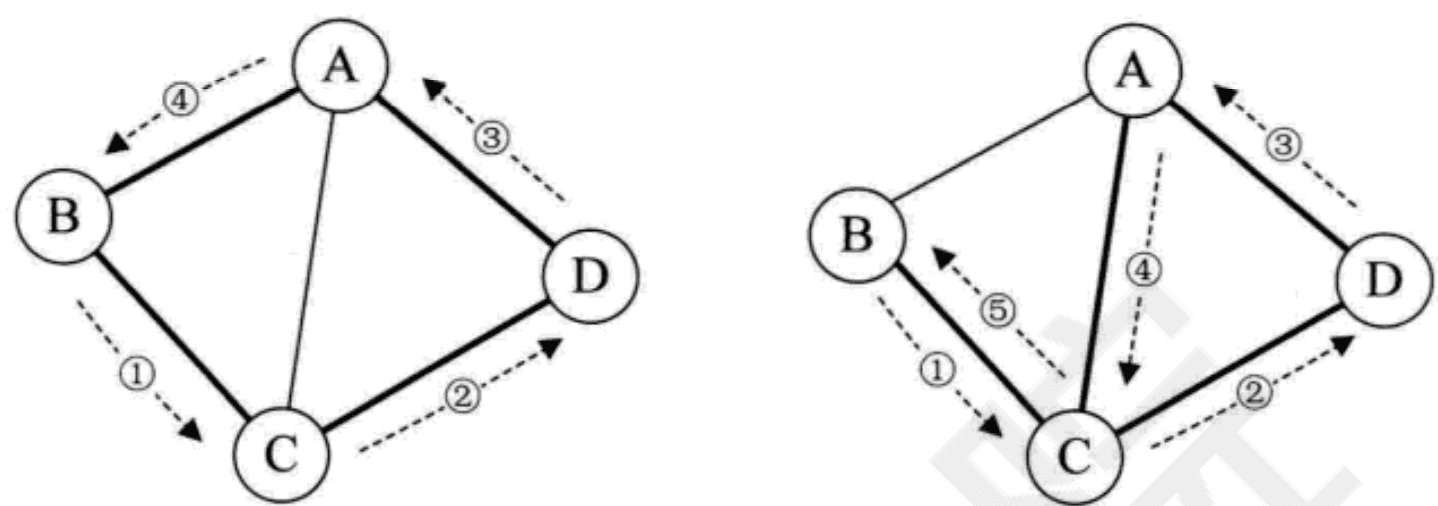
左侧是简单环，右侧不是简单环

10、连通图相关术语

无向图中

  在无向图 G 中，如果从顶点V到顶点V‘有路径，则称V和V‘是连通的。如果对于图中任意两个顶点Vi、Vj∈V，Vi和Vj都是连通的，则称 G 是连通图。无向图中的极大连通子图称为连通分量。连通分量强调：

  • 要是子图；
  • 子图要是连通的；
  • 连通子图含有极大顶点数；
  • 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
有向图中

  在有向图 G 中，如果对于每一对Vi、Vj∈V、Vi≠Vj，从Vi到Vj和从Vj到Vi都存在路径，则称 G 是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。

11、连通图的生成树

  所谓的一个连通图的生成树是一个极小的连通子图，它含有图中全部的 n 个顶点，但只有足以构成一棵树的 n-1 条边。如果一个图有 n 个顶点和小于 n-1 条边，则该图是非连通图。如果它有多于 n-1 条边，则必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。不过有 n-1 条边，并不一定是生成树。
  如果一个有向图恰好有一个顶点的入度为0，其余顶点的入度均为1，则是一颗有向树。对有向树的理解比较容易，所谓入度为0其实就相当于树中的根结点，其余顶点入度为1就是说树的非根节点的双亲只有一个。一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但是有足以构成若干棵不相交的有向弧。

12、图的定义与术语总结

  1. 图按照有无方向分为无向图和有向图。无向图由顶点和边构成，有向图由顶点和弧构成。弧有弧尾和弧头之分。
  2. 图按照边或弧的多少分为稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图，有向图的叫有向完全图。若无重复的边或顶点到自身的边叫简单图。
  3. 图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。
  4. 若图上的边或弧带权，则称为网。
  5. 图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图，有向则是强连通图。图中有子图，若子图极大连通则就是连通分量，有向图则称为强连通分量。
  6. 无向图中连通且 n 个顶点 n-1 条边叫做生成树。有向图中一顶点入度为0，其余顶点入度为1的叫做有向树。一个有向图由若干棵有向树构成生成森林。

二、连通图的最小生成树算法

连通带权无向图
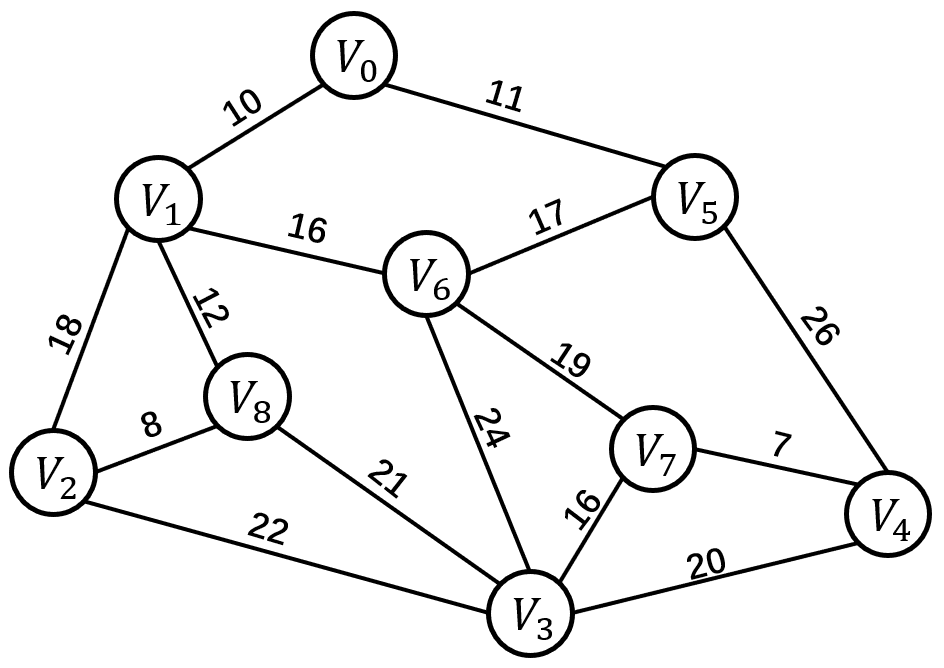
  如上是一个带权值的图，即网结构。所谓的最小成本，就是 n 个顶点，用 n-1 条边把一个连通图连接起来，并使得权值的和最小。

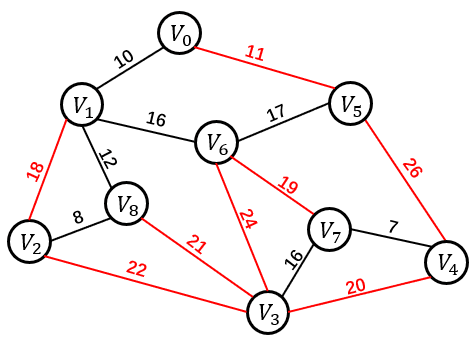
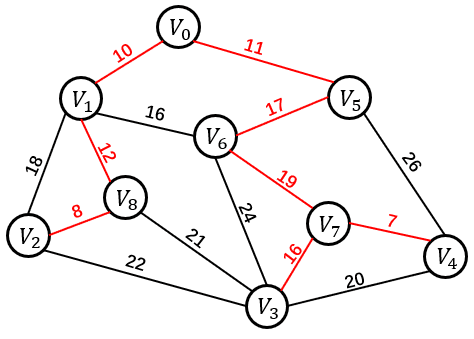
方案一 方案二 方案三
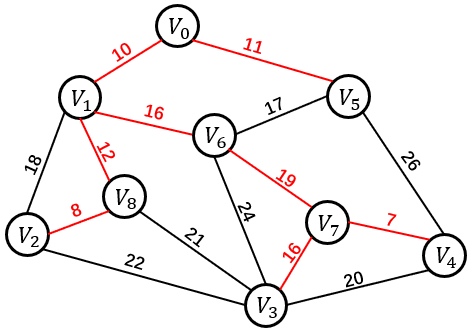11+26+20+22+18+21+24+19=161 8+12+10+11+17+19+16+7=100 8+12+10+11+16+19+7=99

  一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一颗树的 n-1 条边。以上三个方案都是上图的生成树。我们将构造连通网的最小代价生成树称为最小生成树。

1、普里姆算法（Prim）

带权连通图 邻接矩阵

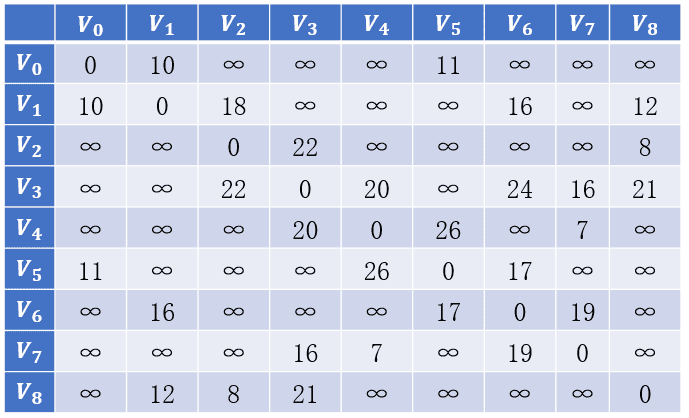  普里姆（Prim）算法的实现过程定义如下：假设 N = (P,{E}) 是连通图，TE 是 N 上最小生成树中边的集合。算法从 U = {u0} (u0∈V)，TE = {} 开始。重复执行以下操作：在所有 u∈U，v∈V-U 的边 (u,v)∈E 中找一条代价最小的边 (u0,v0)并入集合TE，同时v0并入U，直到 U = V 为止。此时 TE 中必有 n-1 条边，则 T = (V,{TE}) 为 N 的最小生成树。由算法代码中的循环嵌套可得知此算法的时间复杂度为 O(n2)

class MGrap {
    final int INFINITY = 65535;//很大很大的数
    int numVertexes = 9;
    int[][] arc = {{0, 10, INFINITY, INFINITY, INFINITY, 11, INFINITY, INFINITY, INFINITY},
            {10, 0, 18, INFINITY, INFINITY, INFINITY, 16, INFINITY, 12},
            {INFINITY, INFINITY, 0, 22, INFINITY, INFINITY, INFINITY, INFINITY, 8},
            {INFINITY, INFINITY, 22, 0, 20, INFINITY, 24, 16, 21},
            {INFINITY, INFINITY, INFINITY, 20, 0, 26, INFINITY, 7, INFINITY},
            {11, INFINITY, INFINITY, INFINITY, 26, 0, 17, INFINITY, INFINITY},
            {INFINITY, 16, INFINITY, INFINITY, INFINITY, 17, 0, 19, INFINITY},
            {INFINITY, INFINITY, INFINITY, 16, 7, INFINITY, 19, 0, INFINITY},
            {INFINITY, 12, 8, 21, INFINITY, INFINITY, INFINITY, INFINITY, 0}};
}

public class GrapTest {
    @Test
    public void test() {
        MGrap g = new MGrap();
        MiniSpanTree_Prim(g);
    }

    public void MiniSpanTree_Prim(MGrap G) {
        int min, i, j, k;
        int[] adjvex = new int[G.numVertexes];
        int[] lowcost = new int[G.numVertexes];
        lowcost[0] = 0;//相当于先将 V0 加入生成树
        adjvex[0] = 0;

        //lowcost[i]永远代表的是边adjvex[i]-->i的代价
        for (i = 1; i < G.numVertexes; i++) {
            lowcost[i] = G.arc[0][i];// V0到其他各顶点的代价，因为目前生成树中只有V0
            adjvex[i] = 0;
        }

        for (i = 1; i < G.numVertexes; i++) {
            min = G.INFINITY;
            j = 1; k = 0;
            while (j < G.numVertexes) {
            	//已经加入到最小生成树中的顶点，其对应的lowcost值为0
                if (lowcost[j] != 0 && lowcost[j] < min) {
                    min = lowcost[j];
                    k = j;
                }
                j++;
            }

            lowcost[k] = 0; //将 Vk 加入生成树
            System.out.println(adjvex[k] + " --> " + k);//打印拥有最小权值的边
			//新的顶点加入到生成树集合后，lowcost和adjvex数组会有相应的变化
            for (j = 1; j < G.numVertexes; j++) {
                if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) {
                    lowcost[j] = G.arc[k][j];
                    adjvex[j] = k;
                }
            }
        }
    }
}

2、克鲁斯卡尔算法（Kruskal）

  普里姆（Prim）算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树。其实，我们也可以直接以边为目标区构建，因为权值是在边上，直接去找最小权值的边来构建生成树也是很自然的想法，但是构建时要考虑是否会形成环路。此时要用到图的存储结构中的边集数据结构。
  克鲁斯卡尔（Kruskal）算法的实现过程定义如下：假设 N = (V,{E}) 是连通网，则令最小生成树的初始状态为只有 n 个顶点而无边的非连通图 T = {V,{}}，图中每个顶点自成一个连通分量。在 E 中选择代价最小的边，若该边依附的顶点落在 T 中不同的连通分量上，则将此边加入到 T 中，否则舍弃此边而选择下一条代价最小的边。依次类推，直至 T 中所有顶点都在同一连通分量上为止。此算法的find函数由边数 e 决定，时间复杂度为 O(log(e))，而外层有一个 for 循环 e 次。所以克鲁斯卡尔算法的时间复杂度为 O(e*log(e))

class Edge {
    int begin;
    int end;
    int weight;

    public Edge(int begin, int end, int weight) {
        this.begin = begin;
        this.end = end;
        this.weight = weight;
    }

    public String toString() {
        return begin + "---" + end + ": " + weight;
    }
}

class MGrap {
    final int INFINITY = 65535;//很大很大的数
    int numVertexes = 9;
    int numEdges = 15;
    int[][] arc = {{0, 10, INFINITY, INFINITY, INFINITY, 11, INFINITY, INFINITY, INFINITY},
            {10, 0, 18, INFINITY, INFINITY, INFINITY, 16, INFINITY, 12},
            {INFINITY, INFINITY, 0, 22, INFINITY, INFINITY, INFINITY, INFINITY, 8},
            {INFINITY, INFINITY, 22, 0, 20, INFINITY, 24, 16, 21},
            {INFINITY, INFINITY, INFINITY, 20, 0, 26, INFINITY, 7, INFINITY},
            {11, INFINITY, INFINITY, INFINITY, 26, 0, 17, INFINITY, INFINITY},
            {INFINITY, 16, INFINITY, INFINITY, INFINITY, 17, 0, 19, INFINITY},
            {INFINITY, INFINITY, INFINITY, 16, 7, INFINITY, 19, 0, INFINITY},
            {INFINITY, 12, 8, 21, INFINITY, INFINITY, INFINITY, INFINITY, 0}};
}

public class GrapTest {
    @Test
    public void test() {
        MGrap g = new MGrap();
        MiniSpanTree_Kruskal(g);
    }

    public void MiniSpanTree_Kruskal(MGrap G) {
        int i, n, m;
        Edge[] edges = new Edge[G.numEdges];//边集数组
        int[] parent = new int[G.numVertexes];

        /*将图的邻接矩阵转换成边集数组edges，并按权值由小到大排序*/
        int j, k;
        for (i = 0, k = 0; i < G.numVertexes; i++) {
            for (j = i + 1; j < G.numVertexes; j++) {
                if (G.arc[i][j] < G.INFINITY) {
                    edges[k++] = new Edge(i, j, G.arc[i][j]);
                }
            }
        }
        Arrays.sort(edges, (e1, e2) -> e1.weight - e2.weight);//Lambda表达式
        //Arrays.stream(edges).forEach(System.out::println);//方法引用

        for (i = 0; i < G.numVertexes; i++) {
            parent[i] = 0;
        }

        for (i = 0; i < G.numEdges; i++) {//循环每条边
        	//若begin和end在不同的连通分量上，则find函数返回的值不相等。
            //相反，若begin和end在同一个连通分量上，则find函数返回的值相等。
            n = find(parent, edges[i].begin);
            m = find(parent, edges[i].end);
            if (n != m) {//此边没有与现生成树形成环
                parent[n] = m;
                //打印拥有最小权值的边
                System.out.println(edges[i].begin + " --> " + edges[i].end);
            }
        }
    }

    //在构建生成树的过程中，所有顶点和已经加入的边会形成多个连通分量。
    //在同一个连通分量上，任意两个顶点按照以下方法，总会返回相同顶点（注意体会）
    int find(int[] parent, int f) {
        while (parent[f] > 0)
            f = parent[f];
        return f;
    }
}

3、对比分析

  对比普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法可知，kruskal算法主要是针对边来展开，当图中的边数少是效率会非常高，所以对于稀疏图有很大的优势；而Prim算法主要是针对顶点来展开，对于稠密图或者边数非常多的情况效率会好一些。

文章作者: YangChongZhi
文章链接: http://yczlab.top/posts/4a73b033.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 YangChongZhi !
Java Algorithm DataStructure
赏
评论
 上一篇
图的最短路径算法 图的最短路径算法
   引言： 图的最短路径问题是求图中两顶点间的最短路径问题。   在网图和非网图中，最短路径的含义不同。由于非网图它没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径；而对于网图来说，最短路径是指两顶点之间经过的边
2021-01-22 Algorithm
Java Algorithm DataStructure
下一篇 
Java8其他新特性之Optional类 Java8其他新特性之Optional类
   引言： 空指针异常是导致Java应用程序失败的最常见原因。以前，为了解决空指针异常，Google公司著名的Guava项目引入了Optional类，Guava通过使用检查空值的方式来防止代码污染，它鼓励程序员写更干净的代码。受到Goog
2021-01-20 Java
Java
  目录