引言:
我是来自成渝赛区UESTC的选手,成渝赛区初赛成绩为0.5646s,当时以为不能晋级复赛,就忘了组队。这里分享我复赛时的方案和代码,复赛练习时成绩为12.1534s,正式复赛时成渝赛区排名21,成功拿到手环(我已经很满足了)。本篇博客对于前排大佬来说毫无用处,仅适用于后排同学一起学习进步。
1. 复赛练习-赛题介绍
1.1 输入信息
输入为包含资金流水的文本文件,每一行代表一次资金交易记录,包含本端账号ID, 对端账号ID, 转账金额,用逗号隔开。
- 本端账号ID和对端账号ID为一个32为的无符号整数
- 转账金额为一个32位的正整数
- 账记录最多为200万条
- 账号A给账号B最多转账一次
输入文件举例如下,其中第一行[1,2,100]表示ID为1的账户给ID为2的账户转账100元:
1,2,100
1,3,100
2,4,90
3,4,19
4,1,95
2,5,95
5,4,90
4,6,30
6,7,29
7,4,28
1.2 输出要求
输出信息为一个文件,包含如下信息:
- 第一行输出:满足限制条件下的循环转账个数。线上数据集经过处理,会保证满足条件的循环转账个数小于2000万。
- 第二行开始:输出所有满足限制条件的循环转账路径详情。输出的循环转账路径要按照指定排序策略进行排序:每条循环转账中,ID(ID转为无符号整数后)最小的第一个输出;总体按照循环转账路径长度升序排序;同一级别的路径长度下循环转账账号ID序列,按照字典序(ID转为无符号整数后)升序排序。
输出举例如下:
3
1,2,4
4,6,7
1,2,5,4
1.3 限制条件
- 循环转账的路径长度最小为3(包含3)最大为7(包含7),例如:账户A给账户B转账,账户B给账户A转账。循环转账的路径长度为2,不满足循环转账条件。
- 转账金额浮动区间约束为[0.2, 3] :循环转账的前后路径的转账金额浮动,不能小于0.2,不能大于3。如账户A转给账户B 转X元,账户B转给账户C转Y元, 那么进行循环检测时,要满足0.2 <= Y/X <= 3的条件。
2. 复赛练习-方案思路
2.1 算法整体框架
- 第一步:使用mmap读取文件并解析好数据,对账户ID做好id映射
- 第二步:构建正向图和反向图,为以下算法打好基础
- 第三步:利用正向图和反向图双向dfs(双向深度搜索),外加多线程并行寻环,同时往结果char数组中写入结果
- 第四步:将char数组的结果写入文件
2.2 算法讲解
以上的步骤中第三步是重点,但是每一步都必不可少(感觉像是在说废话)。
2.2.1 前菜
首先提出一些问题和解决方案,针对这些问题,估计大家都是这么解决的。
1、能不能在寻环的过程中,就能保证环的起点是最小ID值
2、能不能在寻环结束之后,就能保证全部的环是按照长度为第一优先,字典序为第二优先级排好序这两个问题能节省很多多余的操作,并且大部分选手都能解决,所以我还是先从这两个问题开头吧!
这里先介绍一些约定的符号:
- N:表示不重复的账户个数,即节点数
- i:表示账户ID值映射到 0~(N-1) 之间,i∈{0,1,2,…,N-1},这里可以理解为每个账户ID存放在数组中的位置,从0开始
- ID:表示账户(节点)原始的ID,来自于原始的文件数据
针对第一个问题,如果dfs遍历到账户ID为5->4->6->3的环,那么按照赛题的限制要求,我们应该按照3->5->4->6的顺序输出,因为环中的最小ID要放在最前面。那么其实当我们以某个账户ID为起始节点开始dfs时,只要控制后续遍历的ID值是大于这个开始节点的,那么就能保证找到的环都是满足起点是最小ID值。比如:当我们开始寻找以ID为3作为起点的环时,只要控制后续遍历的ID值是大于3的,那么找到的环都是满足起点是最小ID值3。然后再继续寻找以账户ID为4作为起点的环……
针对第二个问题,可以在找完所有的环后,做一个排序。但是其实在dfs遍历寻环的过程中就可以保证其满足字典序。首先对账户ID值做一个排序,保证ID值的相对顺序和ID映射之后的相对顺序一致。比如说有4个账户ID:{5, 11, 8, 13},如果说按照先后出现的顺序做映射,那么将会映射成 ID->i:{5->0, 11->1, 8->2, 13->3}。试想,寻找以i为起点的环,i从0~(N-1)变化,当i为0时,开始找以5为起点的环,然后是以11为起点的环,再然后是以8为起点的环。那这样,全部的环排列当然是无序的。但是如果先对所有的ID排个序,再做映射,ID->:{5->0, 8->1, 11->2, 13->3},其中{5, 8, 11, 13}和{0, 1, 2, 3}的相对大小顺序是相同时。那么在挨个寻环的过程中,环的起点是按顺序排的,但是相同长度的环并非按照字典序排的,这里需要在建图时将每个节点的邻居节点排序,在dfs搜索每个节点的邻居节点时才能保证从小到大的顺序,从而保证找到的环按字典序排好序。这里需要注意的是,要为找到的长度为3,4,5,6,7的环分别建立容器去存储。例如检测到长度为3的环,那么就写到对应的容器中。这个容器可以是int数组,也可以是char数组。
2.2.2 中菜
由于不知道线上数据集的大小,而且复赛规则中取消了每个节点的平均度为10的这个条件,所以图的数据结构,用vector<Node>作为邻接表,用vecotr<Node> G[N]作为整个图,用vector<Node> RG[N]作为反向图(具体请参照后面的代码)。
- 反向图:如果i直接连接到j,那么记录下有哪些节点和j存在以j为终点的直接连接,同样是一个邻接表,只不过是反向记录的。反向图的好处是很大的,可以帮助dfs执行的更快。
2.2.3 压轴菜
2.2.3.1 利用正向图和反向图双向dfs寻环
如果使用dfs寻找长度为7的环,最大递归深度为7,在面对线上如此大的数据集的时候,这个深度可以说非常深,因为层次越大,遍历的节点数目呈指数级上升。能不能不遍历这么多层就可以知道有没有环呢?数组7的最大平均拆分是4+3或者3+4,群里很多选手都说自己的方案是4+3或者几+几。这些数字的意义是啥。见下图: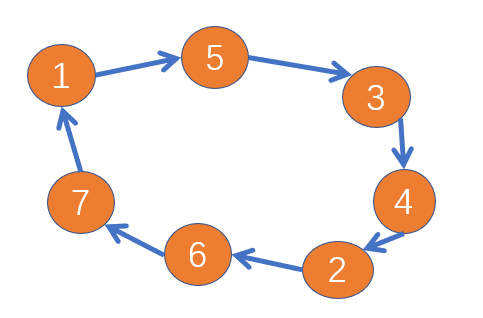
这里有一个环:1->5->3->4->2->6->7,起点为1。
对于一个环来说,从某个位置往后继节点的位置走,和往反方向走,一定会碰到一起。比如1往后继节点走4步到2,然后1反方向走3步也能到2。所以我们可以设置正向dfs递归深度为4,反向dfs递归深度为3。当开始寻找以i为起点的环时,可以先反向走3步,构建能到i能到达的反向路径,用ptp2存这样的路径,转账数额也一同存入;用ptp1存从i反向走2步能到达的反向路径,同样转账数额也一同存入。然后开始从i出发,正向开始遍历,假设第一层dfs遍历到节点k,那么目前的路径为i->k。假设i存在一个长度为3的环{i, k, n},i反向走2步也是到k。而我们已经用ptp1记录了从i反向走两步的所有路径,如果这些路径中存在以k为起点的路段,那我们就找到了一个以i为起点,长度为3的环。接下来,再往后继节点走一步,我们可以通过ptp1获得长度为4的环,通过ptp2获得长度为5的环;再往后继节点走一步,通过ptp2获得长度为6的环;在往后继节点走一步,通过ptp2获得长度为7的环。在进行dfs遍历时,同时要判断转账金额是否满足关于赛题中转账金额的浮动约束。至于如何使用ptp1,ptp2,可以见开源代码部分。
所以整个寻环算法的过程看起来如下: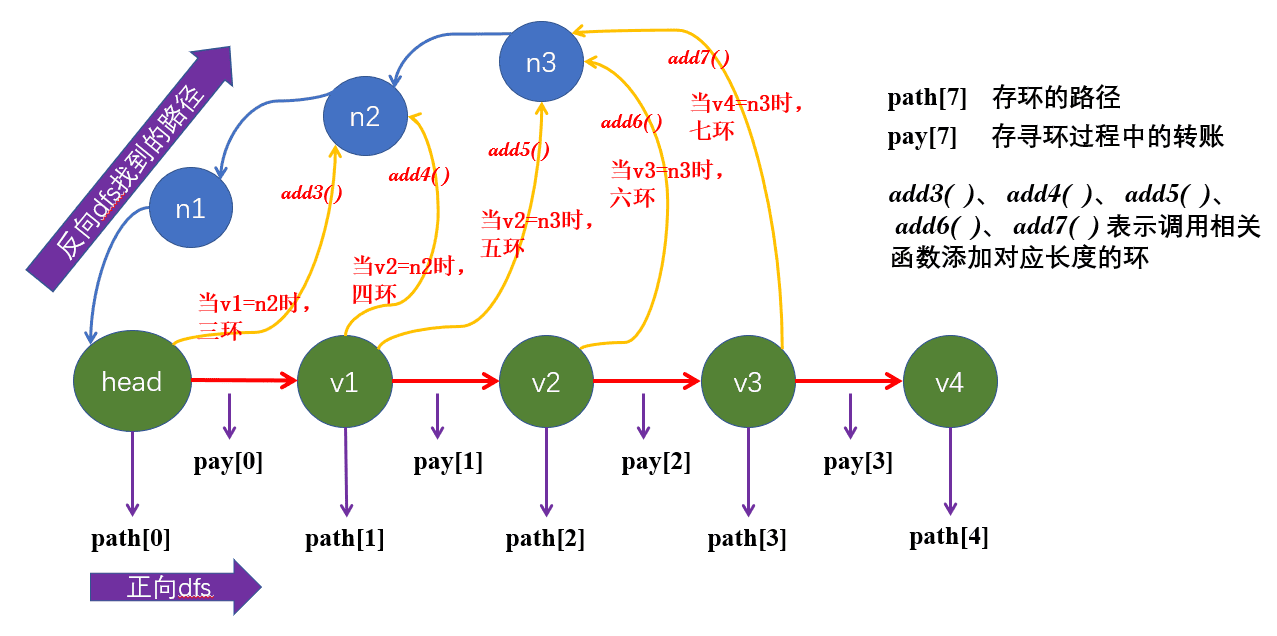
2.2.3.2 双线程并行寻环
很多选手说并行执行是负优化或者提升不大,很可能是没考虑到线程的工作量是否均衡。还有选手说使用并行就result is incorrect,也有可能是每个线程的数组不够大,有些数组被撑爆了,从而导致丢了答案。
前排大佬很可能开了很多线程去同时工作,但是分配给每个线程的工作量必须要均衡,不然很可能工作量少的线程运行完退出后,工作量大的线程还在工作,导致最终算法的执行时间和取决于工作量大的线程的运行时间。
由于摸不透线上数据的分布,所以对于我这种小菜鸟只能勉强使用双线程去实现。一个线程从前往后寻环,另一个线程从后往前寻环,这样两个线程在中间某个节点会碰到一起,此时两个线程的运行时间会差不多,工作量也差别不大。相比于单线程,差不多能提高一倍的成绩。
双线程并行寻环的过程看起来如下: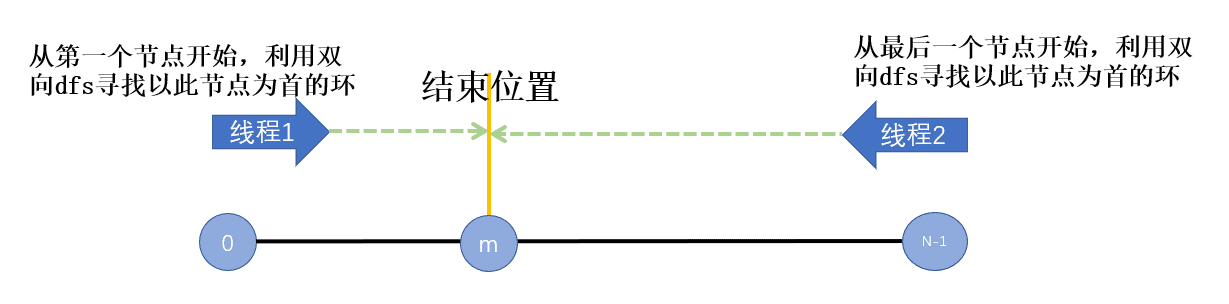
说明1:这里要注意线程2是从大到小寻环,所以在存环的时候也要倒着走,并且在遍历邻居节点时也要倒着遍历。比如我们创建了10M的字符数组char buf3[10*1024*1024]来存放长度为3的环。线程1找到长度为3的环时从buf3的头向尾写入结果,线程2找到长度为3的环时从buf3的尾向头写入结果。其他长度的环同理,为什么这么做,是为了在之后写文件时更快且保证结果排序的正确性。具体请参照代码。
说明2:这里的结束位置肯定是偏左的,因为线程2寻环的首节点id比较大,所以在dfs遍历过程中比这个首节点id大的节点比较少,所寻找的满足条件的环也比较少,可能递归深度没有达到最大就结束了,然后向左移动寻找以id-1为首节点的环。比如,线程2刚开始寻找以最后一个节点为首的环,其实根本找不到满足赛题条件的环,因为其id最大,所以就不可能出现在环首,很快就跳过了最后一个节点。然而线程1是以一个较小的id开始,有较多的节点都比这个id大,所以在遍历过程中比较慢。线程1向右移动的速度比线程2向左移动的速度慢,导致结束位置偏左。正因为以每个节点为首的寻环过程时间开销很难确定,所以想要手动给每个线程提前分配任务就很难做到均分。比如手动将节点数对半分给两个线程,必然是不科学的,并不能达到很好的效果。只有用以上的方法让两个线程自己去把握这个结束位置才能达到较好的效果。当然前排大佬可能使用了更多的线程,任务的分配就更加的复杂,可能使用了自己的调度算法,我这种菜鸟是学不来的,只能做到双线程。
3. 各种细节
3.1 IO篇
- 读数据的时候,顺便把i对应的ID值的字符形式表示出来。有两种办法,第一种,直接从mmap映射到的字符串中截取出来。第二种,自己写个to_char函数,把整型转换为char*,方便写入。我使用的是后者。
- 写入数据直接往字符数组中写,还利用了多线程,那就相当于同时并行处理了写入数据。
- fwrite和mmap到底谁快,有的人说fwrite快,有的人说mmap快。我用的是mmap。对于IO的优化反正对于线上结果影响还挺大的。
3.2 DFS篇
- 前向dfs只要走4步,用5层for循环嵌套的效率远远低于递归写法
- 调整if else if的顺序,把经常发生的情况写在前面,另外switch case的效率高于if else if
- 函数中尽量不要带形参,需要带形参的可以设置为全局变量。
- 根据官方微信推送的优化思路,用一些临时变量有助于减少寻址。
4. 正式复赛-赛题介绍
变更一:
- 循环转账的路径长度最小为3(包含3)最大为8(包含8)
变更二:
- 转账金额变更为浮点数:整数部分大于0,小于2的31次方;小数部分用小于等于2位数的数字表示。如下方式都是正确的表示
- 整数部分.YY 如 1000.53 1000.50 1000.00
- 整数部分.Y 如 1000.5 1000.0
- 整数部分 如 1000
正式复赛要求在两个半小时之内提交结果,有五次提交机会,我太菜了提交了3次都是0%result is incorrect
整体算法思路都以上的思路,采用单线程实现的,由于没有成绩,不知道代码哪个地方有问题,经供参考学习。
5. 赛后感受
- 细节决定排名
- 算法虽好,也要看实现方式(数据结构尽量用数组,new和vector是真的慢)
- C++强无敌,前排没有一个使用python和java的
6. 代码开源
7. 复赛练习 main.cpp
#include <bits/stdc++.h>
#include <unistd.h>
#include <fcntl.h>
#include <sys/mman.h>
using namespace std;
string testFile = "test_data.txt";
string resultFile = "rslt.txt";
typedef struct Node{
int id;
uint money;
bool operator<(const Node &other)const{
return id<other.id;
}
bool operator==(const Node &other)const{
return id==other.id;
}
}Node;
/*构建图需要的变量*/
int account_num = 0;
uint inputs[2*2000000];
uint accts[2*2000000];
vector<Node> G[2000000];
vector<Node> RG[2000000];
/**********************/
/*存放每个账户ID的字符串*/
char account_chars[2000000][12];
short length[2000000];
/**********************/
/*存放结果*/
char buf3[64*1024*1024], *hf3, *tf3; // 64M //线程1通过hf3(head of buf3)从前往后写,线程2通过tf3(tail of buf3)从后往前写
char buf4[64*1024*1024], *hf4, *tf4; // 64M
char buf5[64*1024*1024], *hf5, *tf5; // 64M
char buf6[1024*1024*1024], *hf6, *tf6; // 1024M
char buf7[1468*1024*1024], *hf7, *tf7; // 1468M
int r3_1=0, r4_1=0, r5_1=0, r6_1=0, r7_1=0;
int r3_2=0, r4_2=0, r5_2=0, r6_2=0, r7_2=0;
/**********************/
/*线程锁*/
pthread_mutex_t g_mutex = PTHREAD_MUTEX_INITIALIZER;
/**********************/
/*线程1变量*/
int head_1;
int canReach1_1[2000000][2];
int canReach2_1[2000000][2];
Node layer_1[2000000];
vector<Node> ptp1_1[2000000];
vector<Node> ptp2_1[2000000];
bool vis_1[2000000];
int path_1[7], pay_1[7];
/**********************/
/*线程2变量*/
int head_2;
int canReach1_2[2000000][2];
int canReach2_2[2000000][2];
Node layer_2[2000000];
vector<Node> ptp1_2[2000000];
vector<Node> ptp2_2[2000000];
bool vis_2[2000000];
int path_2[7], pay_2[7];
/**********************/
uint parse_1(char** s){
char *p = *s;
uint val = *(p++) - '0';
while(*p != ',') val = 10*val + *(p++) - '0';
*s = p+1;
return val;
}
uint parse_2(char** s){
char *p = *s;
uint val = *(p++) - '0';
while(*p != '\r' && *p != '\n') val = 10*val + *(p++) - '0';
*s = *p=='\r' ? p+2:p+1;
return val;
}
void parse_to_char(uint a, char *dest, int &k){
int n=0;
do{dest[n++] = a%10+'0';}while((a/=10)>0);
reverse(dest, dest+n);
dest[n++]=',';
length[k]=n;
}
void loadData_and_createGrap(){
int fd = open(testFile.c_str(), O_RDONLY);
int size = lseek(fd, 0, SEEK_END);
char* p_map =(char*)mmap(NULL, size, PROT_READ, MAP_PRIVATE, fd, 0);
close(fd);
char *p = p_map;
int n=0;
uint money[2000000];
while(*p != '\0'){
inputs[n]=parse_1(&p);
inputs[n+2000000]=parse_1(&p);
money[n++]=parse_2(&p);
}
memcpy(accts, inputs, 4*n);
memcpy(accts+n, inputs+2000000, 4*n);
sort(accts, accts+2*n);
account_num = unique(accts, accts+2*n) - accts;
unordered_map<uint, int> idHash;
for(int i=0; i<account_num; ++i) idHash[accts[i]]=i;
Node node;
for(int i=0,a=0,b=0, m=0; i<n; ++i,++m){
a=idHash[inputs[i+0]];
b=idHash[inputs[i+2000000]];
if(a==b) continue;
G[a].push_back(Node{b,money[m]});
RG[b].push_back(Node{a,money[m]});
}
for(int i=0; i<account_num; ++i){
sort(G[i].begin(),G[i].end());
sort(RG[i].begin(),RG[i].end());
parse_to_char(accts[i],account_chars[i], i);
}
munmap(p_map, size);
}
inline bool check(const uint &x, const uint &y){
return x<=5ll*y && y<=3ll*x;
}
/*线程1,从前往后寻环*/
void adpth3_1(){
uint py1=pay_1[0],py3;
int pos = canReach1_1[path_1[1]][1];
for(Node &node:ptp1_1[pos]){
if(!check(py1,node.money)) continue;
py3 = (*find(G[node.id].begin(),G[node.id].end(), Node{path_1[0],0})).money;
if(!check(node.money,py3) || !check(py3,py1)) continue;
memcpy(hf3,account_chars[path_1[0]],length[path_1[0]]); hf3+=length[path_1[0]];
memcpy(hf3,account_chars[path_1[1]],length[path_1[1]]); hf3+=length[path_1[1]];
memcpy(hf3,account_chars[node.id],length[node.id]); hf3+=length[node.id];
*(hf3-1) = '\n';
r3_1++;
}
}
void adpth4_1(){
uint py1=pay_1[0],py2=pay_1[1],py4;
int pos = canReach1_1[path_1[2]][1];
for(Node &node:ptp1_1[pos]){
if(!check(py2,node.money)) continue;
int &n1=node.id;
if(vis_1[n1]) continue;
py4 = (*find(G[node.id].begin(),G[node.id].end(), Node{path_1[0],0})).money;
if(!check(node.money,py4) || !check(py4,py1)) continue;
memcpy(hf4,account_chars[path_1[0]],length[path_1[0]]); hf4+=length[path_1[0]];
memcpy(hf4,account_chars[path_1[1]],length[path_1[1]]); hf4+=length[path_1[1]];
memcpy(hf4,account_chars[path_1[2]],length[path_1[2]]); hf4+=length[path_1[2]];
memcpy(hf4,account_chars[node.id],length[node.id]); hf4+=length[node.id];
*(hf4-1) = '\n';
r4_1++;
}
}
void adpth5_1(){
uint py1=pay_1[0],py2=pay_1[1],py5;
int &pos2 = canReach2_1[path_1[2]][1];
for(Node &node2:ptp2_1[pos2]){
if(!check(py2,node2.money)) continue;
int &n2=node2.id;
if(vis_1[n2]) continue;
int &pos1 = canReach1_1[n2][1];
for(Node &node1:ptp1_1[pos1]){
if(!check(node2.money,node1.money)) continue;
int &n1=node1.id;
if(vis_1[n1]) continue;
py5 = (*find(G[node1.id].begin(),G[node1.id].end(), Node{path_1[0],0})).money;
if(!check(node1.money,py5) || !check(py5,py1)) continue;
memcpy(hf5,account_chars[path_1[0]],length[path_1[0]]); hf5+=length[path_1[0]];
memcpy(hf5,account_chars[path_1[1]],length[path_1[1]]); hf5+=length[path_1[1]];
memcpy(hf5,account_chars[path_1[2]],length[path_1[2]]); hf5+=length[path_1[2]];
memcpy(hf5,account_chars[node2.id],length[node2.id]); hf5+=length[node2.id];
memcpy(hf5,account_chars[node1.id],length[node1.id]); hf5+=length[node1.id];
*(hf5-1) = '\n';
r5_1++;
}
}
}
void adpth6_1(){
uint py1=pay_1[0],py3=pay_1[2],py6;
int pos2 = canReach2_1[path_1[3]][1];
for(Node &node2:ptp2_1[pos2]){
if(!check(py3,node2.money)) continue;
int &n2=node2.id;
if(vis_1[n2]) continue;
int pos1 = canReach1_1[n2][1];
for(Node &node1:ptp1_1[pos1]){
if(!check(node2.money,node1.money)) continue;
int &n1=node1.id;
if(vis_1[n1]) continue;
py6 = (*find(G[node1.id].begin(),G[node1.id].end(), Node{path_1[0],0})).money;
if(!check(node1.money,py6) || !check(py6,py1)) continue;
memcpy(hf6,account_chars[path_1[0]],length[path_1[0]]); hf6+=length[path_1[0]];
memcpy(hf6,account_chars[path_1[1]],length[path_1[1]]); hf6+=length[path_1[1]];
memcpy(hf6,account_chars[path_1[2]],length[path_1[2]]); hf6+=length[path_1[2]];
memcpy(hf6,account_chars[path_1[3]],length[path_1[3]]); hf6+=length[path_1[3]];
memcpy(hf6,account_chars[node2.id],length[node2.id]); hf6+=length[node2.id];
memcpy(hf6,account_chars[node1.id],length[node1.id]); hf6+=length[node1.id];
*(hf6-1) = '\n';
r6_1++;
}
}
}
void adpth7_1(){
uint py1=pay_1[0],py4=pay_1[3],py7;
int pos2 = canReach2_1[path_1[4]][1];
for(Node &node2:ptp2_1[pos2]){
if(!check(py4,node2.money)) continue;
int &n2=node2.id;
if(vis_1[n2]) continue;
int pos1 = canReach1_1[n2][1];
for(Node &node1:ptp1_1[pos1]){
if(!check(node2.money,node1.money)) continue;
int &n1=node1.id;
if(vis_1[n1]) continue;
py7 = (*find(G[node1.id].begin(),G[node1.id].end(), Node{path_1[0],0})).money;
if(!check(node1.money,py7) || !check(py7,py1)) continue;
memcpy(hf7,account_chars[path_1[0]],length[path_1[0]]); hf7+=length[path_1[0]];
memcpy(hf7,account_chars[path_1[1]],length[path_1[1]]); hf7+=length[path_1[1]];
memcpy(hf7,account_chars[path_1[2]],length[path_1[2]]); hf7+=length[path_1[2]];
memcpy(hf7,account_chars[path_1[3]],length[path_1[3]]); hf7+=length[path_1[3]];
memcpy(hf7,account_chars[path_1[4]],length[path_1[4]]); hf7+=length[path_1[4]];
memcpy(hf7,account_chars[node2.id],length[node2.id]); hf7+=length[node2.id];
memcpy(hf7,account_chars[node1.id],length[node1.id]); hf7+=length[node1.id];
*(hf7-1) = '\n';
r7_1++;
}
}
}
void dep4_1(int &u){
vis_1[u] = true;
for(Node &node:G[u]){
if(node.id<=path_1[0] || vis_1[node.id]) continue;
if(!check(pay_1[2],node.money)) continue;
path_1[4]=node.id;
pay_1[3]=node.money;
if(canReach2_1[node.id][0]==path_1[0]){
vis_1[node.id] = 1;
adpth7_1();
vis_1[node.id] = 0;
}
}
vis_1[u] = 0;
}
void dep3_1(int &u){
vis_1[u] = 1;
for(Node &node:G[u]){
if(node.id<=path_1[0] || vis_1[node.id]) continue;
if(!check(pay_1[1],node.money)) continue;
path_1[3]=node.id;
pay_1[2] = node.money;
if(canReach2_1[node.id][0]==path_1[0]){
vis_1[node.id] = 1;
adpth6_1();
vis_1[node.id] = 0;
}
dep4_1(node.id);
}
vis_1[u] = 0;
}
void dep2_1(int &u){
vis_1[u] = 1;
for(Node &node:G[u]){
if(node.id<=path_1[0] || vis_1[node.id]) continue;
if(!check(pay_1[0],node.money)) continue;
path_1[2] = node.id;
pay_1[1] = node.money;
if(canReach1_1[node.id][0]==path_1[0]) adpth4_1();
if(canReach2_1[node.id][0]==path_1[0]){
vis_1[node.id] = 1;
adpth5_1();
vis_1[node.id] = 0;
}
dep3_1(node.id);
}
vis_1[u] = 0;
}
void dep1_1(int &u){
vis_1[u] = 1;
for(Node &node:G[u]){
if(node.id<=u) continue;
path_1[1] = node.id;
pay_1[0] = node.money;
if(canReach1_1[node.id][0]==u) adpth3_1();
dep2_1(node.id);
}
vis_1[u] = 0;
}
void solve_1(){
auto start = chrono::steady_clock::now();
bool flag = false;
memset(vis_1, 0, sizeof(vis_1));
for(int i=0; i<account_num; i++){canReach1_1[i][0]=-1;canReach2_1[i][0]=-1;}
Node tmp;
int headPos,layerSize,layerPos;
while(1){
pthread_mutex_lock(&g_mutex);
if((head_2 - head_1) <= 1) flag=true; //判断后一个顶点是否被线2计算过
head_1++;
pthread_mutex_unlock(&g_mutex);
if(flag) break;
if(G[head_1].size()<1 || RG[head_1].size()<1) continue;
headPos = 0;
layerSize = 0;
for(Node &node1:RG[head_1]){
int &n1 = node1.id;
if(n1<head_1) continue;
for(Node &node2:RG[n1]){
int &n2 = node2.id;
if(n2 <= head_1) continue;
if(canReach1_1[n2][0] != head_1){
canReach1_1[n2][0] = head_1;
canReach1_1[n2][1] = headPos;
ptp1_1[headPos++].clear();
layer_1[layerSize++] = node2;
}
ptp1_1[canReach1_1[n2][1]].push_back(Node{node1.id,node2.money});
}
}
layerPos = 0;
sort(layer_1, layer_1+layerSize);
for(int k=0; k<layerSize; ++k){
Node &node2 = layer_1[k];
for(Node &node3:RG[node2.id]){
int &n3 = node3.id;
if(n3<=head_1) continue;
if(canReach2_1[n3][0] != head_1){
canReach2_1[n3][0] = head_1;
canReach2_1[n3][1] = layerPos;
ptp2_1[layerPos++].clear();
}
ptp2_1[canReach2_1[n3][1]].push_back(Node{node2.id,node3.money});
}
}
path_1[0] = head_1;
dep1_1(head_1);
}
auto end = chrono::steady_clock::now();
double cost_t = chrono::duration<double,std::milli>(end-start).count()/1000;
cout << "solve_1 -const- : " << cost_t << "s" <<" head_1 = "<<head_1<<endl;
}
/*线程2,从后往前寻环,并逆序存入*/
void adpth3_2(){
uint py1=pay_2[0],py3;
int pos = canReach1_2[path_2[1]][1];
for(auto node=ptp1_2[pos].rbegin(); node!=ptp1_2[pos].rend(); ++node){
if(!check(py1,(*node).money)) continue;
py3 = (*find(G[(*node).id].begin(),G[(*node).id].end(), Node{path_2[0],0})).money;
if(!check((*node).money,py3) || !check(py3,py1)) continue;
tf3-=length[(*node).id]; memcpy(tf3,account_chars[(*node).id],length[(*node).id]);
*(tf3+length[(*node).id]-1) = '\n';
tf3-=length[path_2[1]]; memcpy(tf3,account_chars[path_2[1]],length[path_2[1]]);
tf3-=length[path_2[0]]; memcpy(tf3,account_chars[path_2[0]],length[path_2[0]]);
r3_2++;
}
}
void adpth4_2(){
uint py1=pay_2[0],py2=pay_2[1],py4;
int pos = canReach1_2[path_2[2]][1];
for(auto node=ptp1_2[pos].rbegin(); node!=ptp1_2[pos].rend(); ++node){
if(!check(py2,(*node).money)) continue;
int &n1=(*node).id;
if(vis_2[n1]) continue;
py4 = (*find(G[(*node).id].begin(),G[(*node).id].end(), Node{path_2[0],0})).money;
if(!check((*node).money,py4) || !check(py4,py1)) continue;
tf4-=length[(*node).id]; memcpy(tf4,account_chars[(*node).id],length[(*node).id]);
*(tf4+length[(*node).id]-1) = '\n';
tf4-=length[path_2[2]]; memcpy(tf4,account_chars[path_2[2]],length[path_2[2]]);
tf4-=length[path_2[1]]; memcpy(tf4,account_chars[path_2[1]],length[path_2[1]]);
tf4-=length[path_2[0]]; memcpy(tf4,account_chars[path_2[0]],length[path_2[0]]);
r4_2++;
}
}
void adpth5_2(){
uint py1=pay_2[0],py2=pay_2[1],py5;
int &pos2 = canReach2_2[path_2[2]][1];
for(auto node2=ptp2_2[pos2].rbegin(); node2!=ptp2_2[pos2].rend(); ++node2){
if(!check(py2,(*node2).money)) continue;
int &n2=(*node2).id;
if(vis_2[n2]) continue;
int &pos1 = canReach1_2[n2][1];
for(auto node1=ptp1_2[pos1].rbegin(); node1!=ptp1_2[pos1].rend(); ++node1){
if(!check((*node2).money,(*node1).money)) continue;
int &n1=(*node1).id;
if(vis_2[n1]) continue;
py5 = (*find(G[(*node1).id].begin(),G[(*node1).id].end(), Node{path_2[0],0})).money;
if(!check((*node1).money,py5) || !check(py5,py1)) continue;
tf5-=length[(*node1).id]; memcpy(tf5,account_chars[(*node1).id],length[(*node1).id]);
*(tf5+length[(*node1).id]-1) = '\n';
tf5-=length[(*node2).id]; memcpy(tf5,account_chars[(*node2).id],length[(*node2).id]);
tf5-=length[path_2[2]]; memcpy(tf5,account_chars[path_2[2]],length[path_2[2]]);
tf5-=length[path_2[1]]; memcpy(tf5,account_chars[path_2[1]],length[path_2[1]]);
tf5-=length[path_2[0]]; memcpy(tf5,account_chars[path_2[0]],length[path_2[0]]);
r5_2++;
}
}
}
void adpth6_2(){
uint py1=pay_2[0],py3=pay_2[2],py6;
int pos2 = canReach2_2[path_2[3]][1];
for(auto node2=ptp2_2[pos2].rbegin(); node2!=ptp2_2[pos2].rend(); ++node2){
if(!check(py3,(*node2).money)) continue;
int &n2=(*node2).id;
if(vis_2[n2]) continue;
int pos1 = canReach1_2[n2][1];
for(auto node1=ptp1_2[pos1].rbegin(); node1!=ptp1_2[pos1].rend(); ++node1){
if(!check((*node2).money,(*node1).money)) continue;
int &n1=(*node1).id;
if(vis_2[n1]) continue;
py6 = (*find(G[(*node1).id].begin(),G[(*node1).id].end(), Node{path_2[0],0})).money;
if(!check((*node1).money,py6) || !check(py6,py1)) continue;
tf6-=length[(*node1).id]; memcpy(tf6,account_chars[(*node1).id],length[(*node1).id]);
*(tf6+length[(*node1).id]-1) = '\n';
tf6-=length[(*node2).id]; memcpy(tf6,account_chars[(*node2).id],length[(*node2).id]);
tf6-=length[path_2[3]]; memcpy(tf6,account_chars[path_2[3]],length[path_2[3]]);
tf6-=length[path_2[2]]; memcpy(tf6,account_chars[path_2[2]],length[path_2[2]]);
tf6-=length[path_2[1]]; memcpy(tf6,account_chars[path_2[1]],length[path_2[1]]);
tf6-=length[path_2[0]]; memcpy(tf6,account_chars[path_2[0]],length[path_2[0]]);
r6_2++;
}
}
}
void adpth7_2(){
uint py1=pay_2[0],py4=pay_2[3],py7;
int pos2 = canReach2_2[path_2[4]][1];
for(auto node2=ptp2_2[pos2].rbegin(); node2!=ptp2_2[pos2].rend(); ++node2){
if(!check(py4,(*node2).money)) continue;
int &n2=(*node2).id;
if(vis_2[n2]) continue;
int pos1 = canReach1_2[n2][1];
for(auto node1=ptp1_2[pos1].rbegin(); node1!=ptp1_2[pos1].rend(); ++node1){
if(!check((*node2).money,(*node1).money)) continue;
int &n1=(*node1).id;
if(vis_2[n1]) continue;
py7 = (*find(G[(*node1).id].begin(),G[(*node1).id].end(), Node{path_2[0],0})).money;
if(!check((*node1).money,py7) || !check(py7,py1)) continue;
tf7 -= length[(*node1).id]; memcpy(tf7,account_chars[(*node1).id],length[(*node1).id]);
*(tf7+length[(*node1).id]-1) = '\n';
tf7-=length[(*node2).id]; memcpy(tf7,account_chars[(*node2).id],length[(*node2).id]);
tf7-=length[path_2[4]]; memcpy(tf7,account_chars[path_2[4]],length[path_2[3]]);
tf7-=length[path_2[3]]; memcpy(tf7,account_chars[path_2[3]],length[path_2[3]]);
tf7-=length[path_2[2]]; memcpy(tf7,account_chars[path_2[2]],length[path_2[2]]);
tf7-=length[path_2[1]]; memcpy(tf7,account_chars[path_2[1]],length[path_2[1]]);
tf7-=length[path_2[0]]; memcpy(tf7,account_chars[path_2[0]],length[path_2[0]]);
r7_2++;
}
}
}
void dep4_2(int &u){
vis_2[u] = true;
for(auto node=G[u].rbegin(); node!=G[u].rend(); ++node){
if((*node).id<=path_2[0] || vis_2[(*node).id]) continue;
if(!check(pay_2[2],(*node).money)) continue;
path_2[4]=(*node).id;
pay_2[3]=(*node).money;
if(canReach2_2[(*node).id][0]==path_2[0]){
vis_2[(*node).id] = 1;
adpth7_2();
vis_2[(*node).id] = 0;
}
}
vis_2[u] = 0;
}
void dep3_2(int &u){
vis_2[u] = 1;
for(auto node=G[u].rbegin(); node!=G[u].rend(); ++node){
if((*node).id<=path_2[0] || vis_2[(*node).id]) continue;
if(!check(pay_2[1],(*node).money)) continue;
path_2[3]=(*node).id;
pay_2[2] = (*node).money;
if(canReach2_2[(*node).id][0]==path_2[0]){
vis_2[(*node).id] = 1;
adpth6_2();
vis_2[(*node).id] = 0;
}
dep4_2((*node).id);
}
vis_2[u] = 0;
}
void dep2_2(int &u){
vis_2[u] = 1;
for(auto node=G[u].rbegin(); node!=G[u].rend(); ++node){
if((*node).id<=path_2[0] || vis_2[(*node).id]) continue;
if(!check(pay_2[0],(*node).money)) continue;
path_2[2] = (*node).id;
pay_2[1] = (*node).money;
if(canReach1_2[(*node).id][0]==path_2[0]) adpth4_2();
if(canReach2_2[(*node).id][0]==path_2[0]){
vis_2[(*node).id] = 1;
adpth5_2();
vis_2[(*node).id] = 0;
}
dep3_2((*node).id);
}
vis_2[u] = 0;
}
void dep1_2(int &u){
vis_2[u] = 1;
for(auto node=G[u].rbegin(); node!=G[u].rend(); ++node){
if((*node).id<=u) continue;
path_2[1] = (*node).id;
pay_2[0] = (*node).money;
if(canReach1_2[(*node).id][0]==u) adpth3_2();
dep2_2((*node).id);
}
vis_2[u] = 0;
}
void solve_2(){
auto start = chrono::steady_clock::now();
bool flag = false;
memset(vis_2, 0, sizeof(vis_2));
for(int i=0; i<account_num; i++){canReach1_2[i][0]=-1;canReach2_2[i][0]=-1;}
Node tmp;
int headPos,layerSize,layerPos;
while(1){
pthread_mutex_lock(&g_mutex);
if((head_2 - head_1) <= 1) flag=true; //判断前一个顶点是否被线1计算过
head_2--;
pthread_mutex_unlock(&g_mutex);
if(flag) break;
if(G[head_2].size()<1 || RG[head_2].size()<1) continue;
headPos = 0;
layerSize = 0;
for(Node &node1:RG[head_2]){
int &n1 = node1.id;
if(n1<head_2) continue;
for(Node &node2:RG[n1]){
int &n2 = node2.id;
if(n2 <= head_2) continue;
if(canReach1_2[n2][0] != head_2){
canReach1_2[n2][0] = head_2;
canReach1_2[n2][1] = headPos;
ptp1_2[headPos++].clear();
layer_2[layerSize++] = node2;
}
ptp1_2[canReach1_2[n2][1]].push_back(Node{node1.id,node2.money});
}
}
layerPos = 0;
sort(layer_2, layer_2+layerSize);
for(int k=0; k<layerSize; ++k){
Node &node2 = layer_2[k];
for(Node &node3:RG[node2.id]){
int &n3 = node3.id;
if(n3<=head_2) continue;
if(canReach2_2[n3][0] != head_2){
canReach2_2[n3][0] = head_2;
canReach2_2[n3][1] = layerPos;
ptp2_2[layerPos++].clear();
}
ptp2_2[canReach2_2[n3][1]].push_back(Node{node2.id,node3.money});
}
}
path_2[0] = head_2;
dep1_2(head_2);
}
auto end = chrono::steady_clock::now();
double cost_t = chrono::duration<double,std::milli>(end-start).count()/1000;
cout << "solve_2 -const- : " << cost_t << "s" << endl;
}
void save(){
char tmp[20];
int m=sprintf(tmp,"%d\n",r3_1+r4_1+r5_1+r6_1+r7_1 + r3_2+r4_2+r5_2+r6_2+r7_2);
int n=m;
n += sizeof(buf3) - (tf3 - hf3); //存放长度为3的环所用的字节数
n += sizeof(buf4) - (tf4 - hf4);
n += sizeof(buf5) - (tf5 - hf5);
n += sizeof(buf6) - (tf6 - hf6);
n += sizeof(buf7) - (tf7 - hf7);
int fd = open(resultFile.c_str(), O_RDWR|O_CREAT, 0666);
lseek(fd, n-1, SEEK_SET);
write(fd, "", 1);
char* p_mmap =(char*)mmap(NULL, n, PROT_WRITE, MAP_SHARED, fd, 0);
char* p = p_mmap;
memcpy(p, tmp, m); p+=m; //写入找到的环的总个数
int len = hf3-buf3;
memcpy(p, buf3, len); p+=len;
len = buf3 + sizeof(buf3) - tf3;
memcpy(p, tf3, len); p+=len;
len = hf4-buf4;
memcpy(p, buf4, len); p+=len;
len = buf4 + sizeof(buf4) - tf4;
memcpy(p, tf4, len); p+=len;
len = hf5-buf5;
memcpy(p, buf5, len); p+=len;
len = buf5 + sizeof(buf5) - tf5;
memcpy(p, tf5, len); p+=len;
len = hf6-buf6;
memcpy(p, buf6, len); p+=len;
len = buf6 + sizeof(buf6) - tf6;
memcpy(p, tf6, len); p+=len;
len = hf7-buf7;
memcpy(p, buf7, len); p+=len;
len = buf7 + sizeof(buf7) - tf7;
memcpy(p, tf7, len); p+=len;
*p = '\0';
munmap(p_mmap, n);
close(fd);
}
int main(int argc, char* argv[]){
clock_t startTime = clock();
loadData_and_createGrap();
clock_t endTime = clock();
cout << "LoadDataAndCreateGraph: " << (float)(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
hf3=buf3;tf3=buf3+sizeof(buf3);
hf4=buf4;tf4=buf4+sizeof(buf4);
hf5=buf5;tf5=buf5+sizeof(buf5);
hf6=buf6;tf6=buf6+sizeof(buf6);
hf7=buf7;tf7=buf7+sizeof(buf7);
head_1 = -1;
head_2 =account_num;
auto start = chrono::steady_clock::now();
vector<thread> threadpool(2);
threadpool[0] = thread(&solve_1);
threadpool[1] = thread(&solve_2);
threadpool[0].join();
threadpool[1].join();
auto end = chrono::steady_clock::now();
double cost_t = chrono::duration<double,std::milli>(end-start).count()/1000;
cout << "compute : " << cost_t << "s" << endl;
startTime = clock();
save();
endTime = clock();
cout << "save: " << (float)(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
cout<<endl;
cout<<"p3_1 = "<<r3_1<<endl;
cout<<"p4_1 = "<<r4_1<<endl;
cout<<"p5_1 = "<<r5_1<<endl;
cout<<"p6_1 = "<<r6_1<<endl;
cout<<"p7_1 = "<<r7_1<<endl<<endl;
cout<<"p3_2 = "<<r3_2<<endl;
cout<<"p4_2 = "<<r4_2<<endl;
cout<<"p5_2 = "<<r5_2<<endl;
cout<<"p6_2 = "<<r6_2<<endl;
cout<<"p7_2 = "<<r7_2<<endl<<endl;
int all = r3_1+r4_1+r5_1+r6_1+r7_1;
all += r3_2+r4_2+r5_2+r6_2+r7_2;
cout<<"all_loops = "<<all<<endl;
exit(0);
}


