KMP模式匹配算法

Java

发布日期: 2021-01-16

更新日期: 2022-07-31

文章字数: 2.7k

阅读时长: 11 分

阅读次数:

引言：

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。
转自：如何更好地理解和掌握 KMP 算法

字符串的模式匹配是一种常用的运算。所谓模式匹配,可以简单地理解为在目标(字符串)中寻找一个给定的模式(也是字符串)，返回目标和模式匹配的第一个子串的首字符位置。通常目标串比较大，而模式串则比较短小。
比较暴力的解法是，在大循环中遍历主串的每个字符，并以此字符为首，挨个与模式字符串中的每个字符依次比较，若全能匹配上，则返回该首字符所在位置；若不能全匹配上，则在主字符串中循环下一个字符作为首字符重新与模式字符串依次比较。这种方式不仅慢，而且慢，而且还慢。KMP算法是一种改进的字符串匹配算法，其关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

KMP 算法

先解释一下字符串的前缀和后缀。如果字符串A和B，存在A=BS，其中S是任意的非空字符串，那就称B为A的前缀。例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。同样可以定义后缀A=SB，其中S是任意的非空字符串，那就称B为A的后缀，例如，”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。要注意的是，字符串本身并不是自己的前缀、后缀。

KMP算法的核心，是一个被称为**部分匹配表(Partial Match Table)**的数组。我觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后，仍然搞不懂PMT中的值代表了什么意思。这里我们抛开所有的枝枝蔓蔓，先来解释一下这个数据到底是什么。
对于字符串“abababca”，它的PMT如下表所示：


char	a	b	a	b	a	b	c	a
index	0	1	2	3	4	5	6	7
value	0	0	1	2	3	4	0	1

就像例子中所示，如果待匹配的模式字符串有8个字符，那么PMT就会有8个值。那么PMT中各个值的意思是什么呢？PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。再比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}，两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。
解释清楚这个表是什么之后，我们再来看如何使用这个表来加速字符串的查找，以及这样用的道理是什么。如下图所示，要在主字符串”ababababca”中查找模式字符串”abababca”。如果在模式字符串的 j 处字符不匹配，那么由于前边所说的模式字符串 PMT 的性质，主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配，也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。上面也解释了，模式字符串从 0 到 j−1 ，在这个例子中就是”ababab”，其前缀集合与后缀集合的交集的最长元素为”abab”，长度为4。所以就可以断言，主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的，即长度为 4 的后缀与前缀相同。这样一来，我们就可以将这些字符段的比较省略掉。具体的做法是，保持i指针不动，然后将j指针指向模式字符串的PMT[j −1]位即可。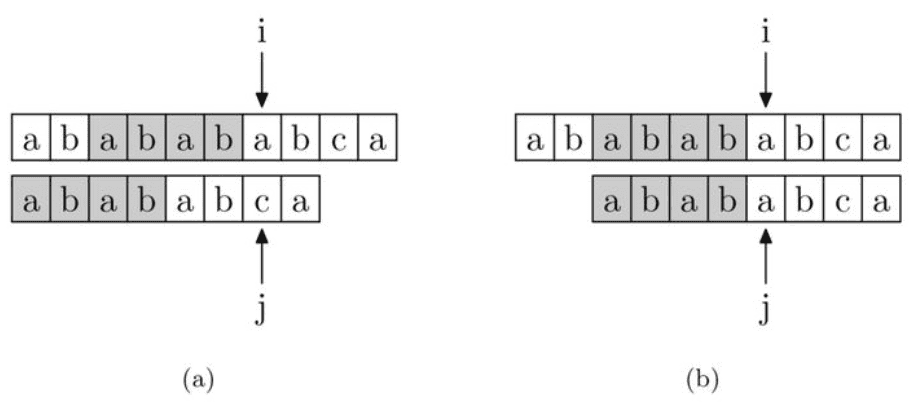
匹配过程示意图
简而言之，以图中的例子来说，主字符串在 i 处失配，那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位，它的前4位前缀和后4位后缀是相同的，所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。
有了上面的思路，我们就可以使用PMT算法加速字符串的查找了。我们看到如果模式字符串是在 j 位失配那么影响 j 指针回溯的位置的其实是第 j−1 位的PMT值，所以为了编程的方便，我们不直接使用PMT数组，而是将PMT数组向后偏移一位，将偏移后新得到的数组称为 next 数组。但是注意：在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。本例中的next数组如下表所示：


char	a	b	a	b	a	b	c	a
index	0	1	2	3	4	5	6	7
pmt	0	0	1	2	3	4	0	1
next	-1	0	0	1	2	3	4	0

下面给出根据next数组进行字符串匹配加速的字符串匹配程序。

int KMP(char * t, char * p)
{
	int i = 0;
    int j = 0;
	while (i < strlen(t) && j < strlen(p)) {
		if (j == -1 || t[i] == p[j])
		{
        	i++;
            j++;
		}
	 	else
        	j = next[j];
    }
    if (j == strlen(p))
    	return i - j;
    else
    	return -1;
}

讲到这里，其实KMP算法的主体就已经讲解完了。你会发现，其实KMP算法的动机是很简单的，解决的方案也很简单。远没有很多教材和算法书里所讲的那么乱七八糟，只要搞明白了PMT的意义，其实整个算法都迎刃而解。但是现在还有一个问题，如何快速求得next数组。其实，求next数组的过程也完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。具体来说，就是从模式字符串的第一位(注意，不包括第0位)开始对自身进行匹配运算。在任一位置，能匹配的最长长度就是当前位置的next值。如下图所示：（默认next[0]=-1，next[1]=0）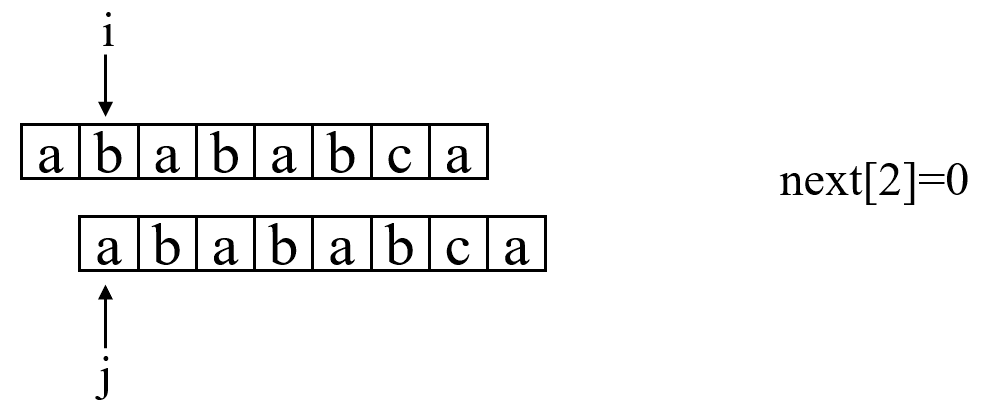
(a)
(b)
(c)
(d)
(e)
(f)

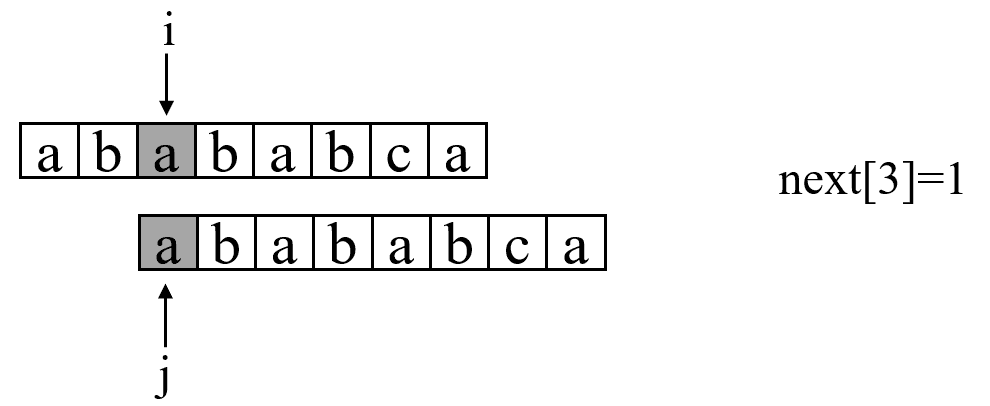
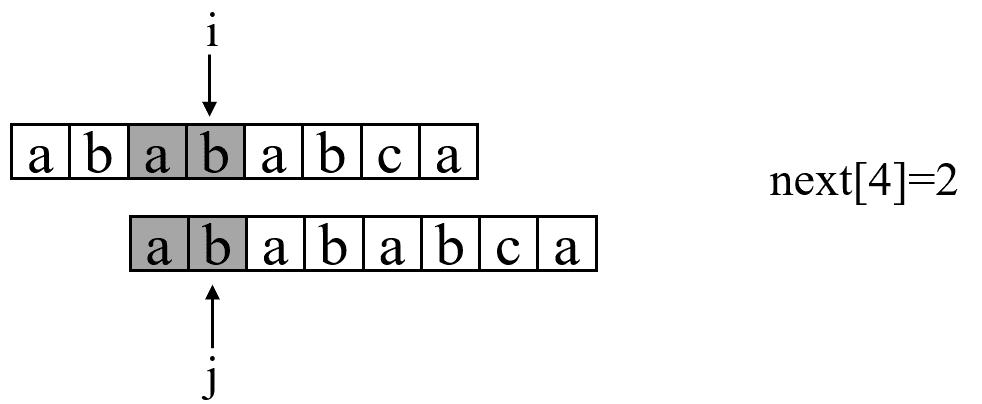
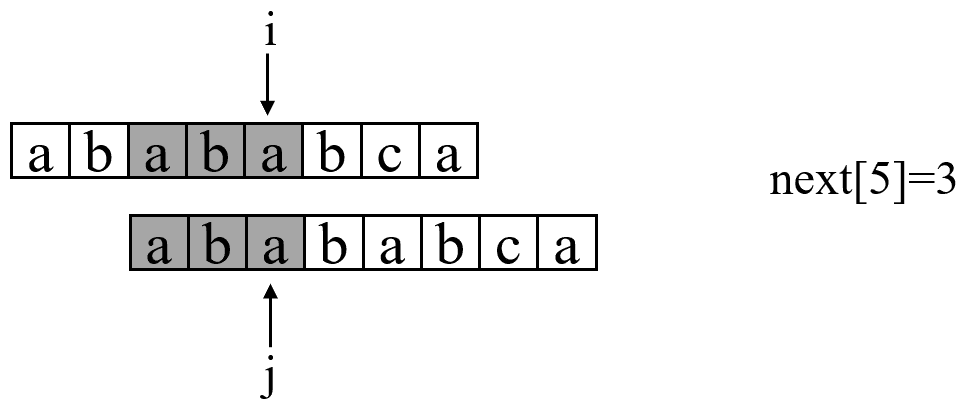
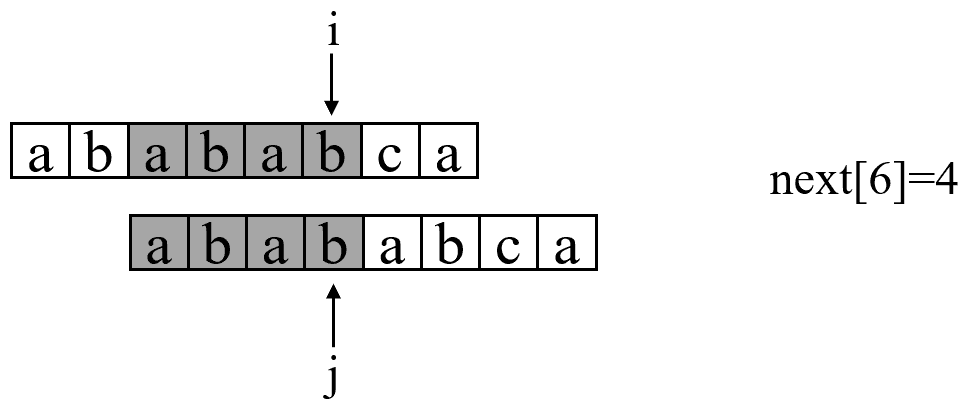
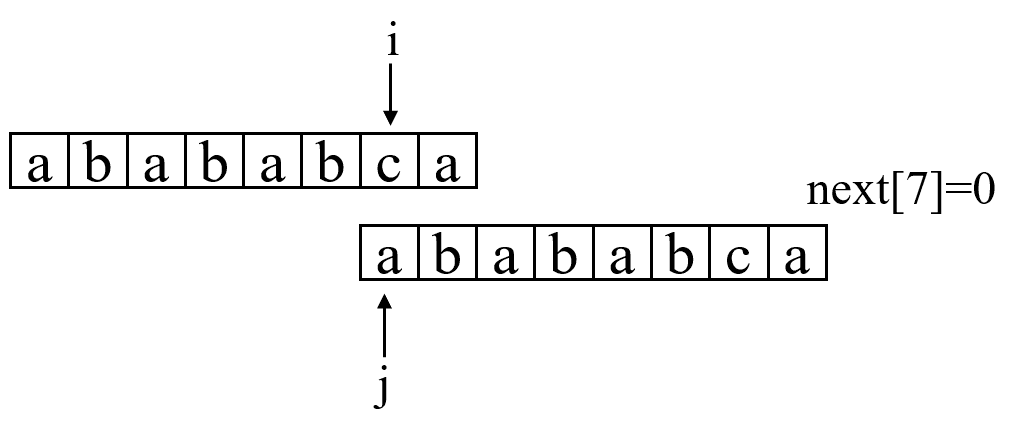
求next数组值的程序如下。

void getNext(char * p, int * next)
{
	next[0] = -1;
	int i = 0, j = -1;

	while (i < strlen(p)) {
		if (j == -1 || p[i] == p[j])
		{
			++i;
			++j;
			next[i] = j;
		}
		else
			j = next[j];
	}
}

至此，KMP算法就全部介绍完了。

java程序示例：

public class KMP {
    @Test
    public void test(){
        String mainStr = "dhakshdakdhasjdhjahsdjh";
        String subStr = "hasjdh";
        int res1 = KMP1(mainStr, subStr);
        int res2 = KMP2(mainStr, subStr);
        System.out.println(res1);
        System.out.println(res2);
    }

    /* KMP模式匹配算法，从前往后匹配 */
    public int KMP1(String mainStr, String subStr) {
        char[] str = mainStr.toCharArray();
        char[] sub = subStr.toCharArray();
        //构造next数组[-1, 0, ......]。部分匹配表PMT
        int[] next = new int[sub.length + 1];
        next[0] = -1;
        int i = 0, j = -1;
        while (i < sub.length) {
            if (j == -1 || sub[i] == sub[j]) {
                ++i;
                ++j;
                next[i] = j;
            } else {
                j = next[j];
            }
        }

        i = 0;
        j = 0;
        while (i < str.length && j < sub.length) {
            if (j == -1 || str[i] == sub[j]) {
                ++i;
                ++j;
            } else {
                j = next[j];
            }
        }
        if (j == sub.length) {
            return i - j;
        }
        return -1;
    }

    /* KMP模式匹配算法，从后往前匹配 */
    public int KMP2(String mainStr, String subStr) {
        char[] str = mainStr.toCharArray();
        char[] sub = subStr.toCharArray();
        //构造next数组[......, length-1, length]。部分匹配表PMT
        int[] next = new int[sub.length + 1];
        next[sub.length] = sub.length;
        int i = sub.length - 1;
        int j = sub.length;
        while (i > -1) {
            if (j == sub.length || sub[i] == sub[j]) {
                --i;
                --j;
                next[i+1] = j;//避免出现next[-1]，将结果往后存。
            } else {
                j = next[j+1];
            }
        }

        i = str.length - 1;
        j = sub.length - 1;
        while (i > -1 && j > -1) {
            if (j == sub.length || str[i] == sub[j]) {
                --i;
                --j;
            } else {
                j = next[j+1];
            }
        }
        if (j == -1) {
            return i - j;
        }
        return -1;
    }
}

KMP改进

public class KMP {
    @Test
    public void test(){
        String mainStr = "dhakshdakdhasjdhjahsdj";
        String subStr = "hasjdh";
        int res1 = KMP1(mainStr, subStr);
        int res2 = KMP2(mainStr, subStr);
        System.out.println(res1);
        System.out.println(res2);
    }

    /* KMP模式匹配算法，从前往后匹配 */
    public int KMP1(String mainStr, String subStr) {
        char[] str = mainStr.toCharArray();
        char[] sub = subStr.toCharArray();
        int[] next = new int[sub.length + 1];
        next[0] = -1;
        int i = 0, j = -1;
        while (i < sub.length) {
            if (j == -1 || sub[i] == sub[j]) {
                ++i;
                ++j;
                //为了在后续匹配时，加快回溯（注意体会不同点）
                if (i < sub.length && sub[i] == sub[j]) {
                    next[i] = next[j];
                } else {
                    next[i] = j;
                }
            } else {
                j = next[j];
            }
        }

        i = 0;
        j = 0;
        while (i < str.length && j < sub.length) {
            if (j == -1 || str[i] == sub[j]) {
                ++i;
                ++j;
            } else {
                j = next[j];
            }
        }
        if (j == sub.length) {
            return i - j;
        }
        return -1;
    }

    /* KMP模式匹配算法，从后往前匹配 */
    public int KMP2(String mainStr, String subStr) {
        char[] str = mainStr.toCharArray();
        char[] sub = subStr.toCharArray();
        int[] next = new int[sub.length + 1];
        next[sub.length] = sub.length;
        int i = sub.length - 1;
        int j = sub.length;
        while (i > -1) {
            if (j == sub.length || sub[i] == sub[j]) {
                --i;
                --j;
                //为了在后续匹配时，加快回溯（注意体会不同点）
                if (i > -1 && sub[i] == sub[j]) {
                    next[i + 1] = next[j + 1];
                } else {
                    next[i + 1] = j;
                }
            } else {
                j = next[j+1];
            }
        }

        i = str.length - 1;
        j = sub.length - 1;
        while (i > -1 && j > -1) {
            if (j == sub.length || str[i] == sub[j]) {
                --i;
                --j;
            } else {
                j = next[j+1];
            }
        }
        if (j == -1) {
            return i - j;
        }
        return -1;
    }
}