滑动窗口的最大值

Algorithm

发布日期: 2021-02-04

更新日期: 2022-07-31

文章字数: 1.7k

阅读时长: 7 分

阅读次数:

引言：

LeetCode中遇到的一道题，记录一下。
转自求滑动窗口的最大值

问题定义

给定一个数组 nums 和滑动窗口的大小 k，要求找出所有滑动窗口中的最大值。

(可以假设 k 总是有效的，在输入数组不为空的情况下，1 ≤ k ≤ 输入数组的长度)

解题思路 1

单调队列
设窗口区间为 [i,j]，最大值为 x_j。当窗口向前移动一格，则区间变为 [i+1, j+1]，即添加了 nums[j+1]，删除了 nums[i]。若只向窗口 [i,j] 右边添加数字 nums[j+1]，则新窗口最大值可以通过一次对比使用O(1)时间得到，即：x_j+1 = max(x_j, nums[j+1])。但是由于删除的 nums[i] 可能恰好是窗口内唯一的最大值 x_j，因此不能通过以上方法直接计算 x_j+1，而必须使用 O(j-i)时间，遍历整个窗口区间获取最大值，即：x_j+1 = max(nums[i+1],···,nums[j+1])。
根据以上分析可知，可得暴力法的时间复杂度为 O((n-k+1)k)≈O(nk)。①设数组nums的长度为n，则共有(n-k+1)个窗口；②获取每个窗口的最大值需线性遍历，时间复杂度为O(k)。本题的难点是：如何在每次窗口滑动后，将“获取窗口内最大值”的时间复杂度从O(k)降低至O(1)。回忆一下LeetCode中的这道题面试题30. 包含min函数的栈，其使用单调栈实现了随意入栈，出栈情况下的 O(1) 时间获取栈内最小值。本题同理，不同点在于“出栈操作”删除的是“列表尾部元素”，而“滑动窗口”删除的是“列表首部元素”。
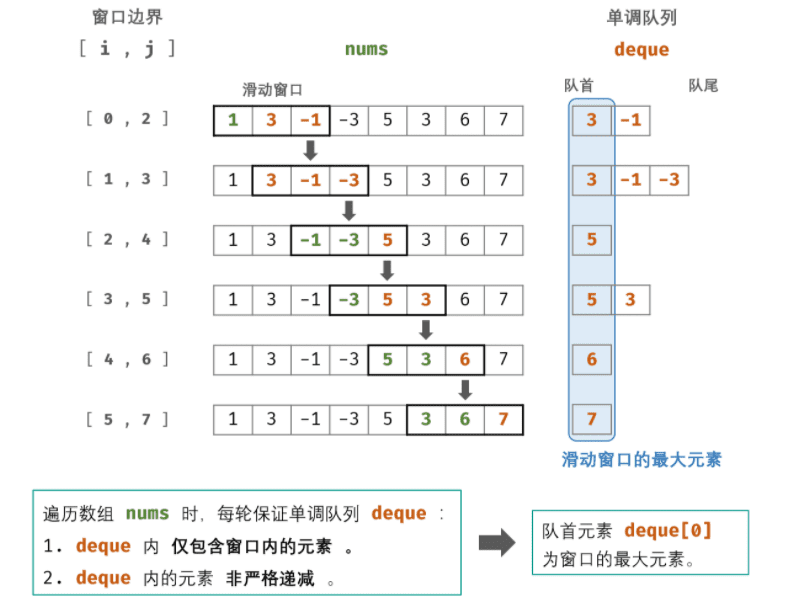
窗口对应的数据结构为双端队列，本题使用单调队列解决以上问题。遍历数组时，每轮保证单调队列 deque：

deque 内仅包含窗口内的元素 ⇒ 每轮窗口滑动移除了元素 nums[i]，需将 deque 内的对应元素一起删除。

deque 内的元素非严格递减 ⇒ 每轮窗口滑动添加了元素[j+1]，需将 deque 内所有小于nums[j+1]的元素删除。

算法流程

初始化：双端队列deque，结果列表res，数组长度n;
滑动窗口：左边界范围 i ∈ [1-k, n-k+1]，右边界范围 j ∈ [0, n-1];
- 若 i > 0 且队首元素 deque[0] = 被删除元素nums[i-1]，则队首元素出队；
- 删除 deque 内所有小于nums[j]的元素，以保持 deque 递减;
- 将 nums[j] 添加至 deque 尾部;
- 若已形成窗口（即 i ≥ 0），将窗口最大值（即队首元素deque[0]）添加至列表 res 中。
返回结果 res

流程示意图

复杂度分析

时间复杂度 O(n)：其中 n 为数组 nums 长度；线性遍历 nums 占用 O(N)；每个元素最多仅入队和出队一次，因此单调队列 deque 占用 O(2N)。
空间复杂度 O(k)：双端队列 deque 中最多同时存储 k 个元素（即窗口大小）。

参考代码

public class LeetCodeTest {
    @Test
    public void  test() {
        int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
        int k = 3;
        int[] ans = maxSlidingWindow(nums, k);
        System.out.println(Arrays.toString(ans));
    }

    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 0 || k == 0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        for (int j = 0, i = 1 - k; j < nums.length; i++, j++) {
            if (i > 0 && deque.peekFirst() == nums[i - 1]) {
                deque.removeFirst(); // 删除 deque 中对应的 nums[i-1]
            }
            while (!deque.isEmpty() && deque.peekLast() < nums[j]) {
                deque.removeLast(); //保持 deque 递减
            }
            deque.addLast(nums[j]);
            if (i >= 0) {
                res[i] = deque.peekFirst(); // 记录窗口最大值
            }
        }
        return res;
    }

    // 可将未形成窗口和形成的窗口分开
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(nums.length == 0 || k == 0) return new int[0];
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k + 1];
        for(int i = 0; i < k; i++) { // 未形成窗口
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
        }
        res[0] = deque.peekFirst();
        for(int i = k; i < nums.length; i++) { // 形成窗口后
            if(deque.peekFirst() == nums[i - k])
                deque.removeFirst();
            while(!deque.isEmpty() && deque.peekLast() < nums[i])
                deque.removeLast();
            deque.addLast(nums[i]);
            res[i - k + 1] = deque.peekFirst();
        }
        return res;
    }
}

解题思路 2

优先队列(大根堆) + 延迟删除
参考“滑动窗口求中位数”的算法（双优先队列(大根堆)+ 延迟删除）
由于优先队列是不支持移除非堆顶元素，因此可以考虑使用延迟删除的办法。即：当我们需要移除优先队列中的某个元素时，我们只是将这个删除操作记录下来，而不是立即马上真的去删除这个元素。当这个元素出现在堆顶时，我们再考虑真正去删除这个元素。
延迟删除使用到的辅助数据结构一般为哈希表delayed，其中每个键值对(num,freq)表示 num 还需要被删除 freq 次。优先队列 + 延迟删除有非常多种设计方式，体现在延迟删除的时机选择上。这里我们使用一种比较容易编写代码的设计方式。

public class LeetCodeTest {
    @Test
    public void  test() {
        int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
        int k = 3;
        int[] ans = maxSlidingWindow(nums, k);
        System.out.println(Arrays.toString(ans));
    }

    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 0 || k == 0) return new int[0];
        PriorityDelayQueue heap = new PriorityDelayQueue(k);
        for (int i = 0; i < k; i++) {
            heap.insert(nums[i]);
        }
        int[] ans = new int[nums.length - k + 1];
        ans[0] = heap.getMax();
        for (int i = k; i < nums.length; i++) {
            heap.insert(nums[i]);
            heap.erase(nums[i - k]);
            ans[i - k + 1] = heap.getMax();
        }
        return ans;
    }
}

/*优先队列（大根堆） + 延迟删除*/
class PriorityDelayQueue {
    // 大根堆，堆顶元素是最大值
    private Queue<Integer> heap;
    // 哈希表，记录需要延迟删除的元素，key为元素，value为需要删除的次数
    private Map<Integer, Integer> delayed;
    // 窗口大小
    private int k;
    // 该数据结构中所维护的有效元素个数，需要扣除被延迟删除的元素
    private int size;

    public PriorityDelayQueue(int k) {
        this.heap = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2 - o1;
            }
        });
        this.delayed = new HashMap<>();
        this.k = k;
        int size = 0;
    }

    public int getMax() {
        prune();// 保证堆顶元素不是需要延迟删除的元素
        return heap.peek();
    }

    public void insert(int num) {
        heap.offer(num);
        ++size;
    }

    public void erase(int num) {
        delayed.put(num, delayed.getOrDefault(num, 0) + 1);
        --size;
    }

    // 不断弹出 heap 的堆顶元素，并且更新哈希表
    public void prune() {
        while (!heap.isEmpty()) {
            int num = heap.peek();
            if (delayed.containsKey(num)) {
                delayed.put(num, delayed.get(num) - 1);
                if (delayed.get(num) == 0) {// 该数不再被延迟删除时，直接从delayed中删除该数
                    delayed.remove(num);
                }
                heap.poll();
            } else {
                break;
            }
        }
    }
}